Расчёт панелей из композиционных материалов, страница 6

Приведенные коэффициенты Q_ij  используются для построения матрицы жёсткости. Эти коэффициенты идентичны коэффициентам С_ij.

Здесь:

                             (18.8).

Для трансверсально-изотропного слоя имеющего одинаковые свойства в направлениях 2 и 3

v₁₂ =  v₁₃,   G₁₂ = G₁₃,   E₂₂ = E₃₃.

Для приближённых расчётов можно пользоваться более простыми соотношениями:

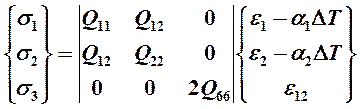                                                   (18.9)

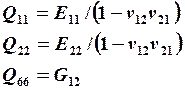                                                                                    (18.10)

В координатной системе х – у – z  уравнение (18.7) с учётом (18.4) и (18.5) выглядит следующим образом:

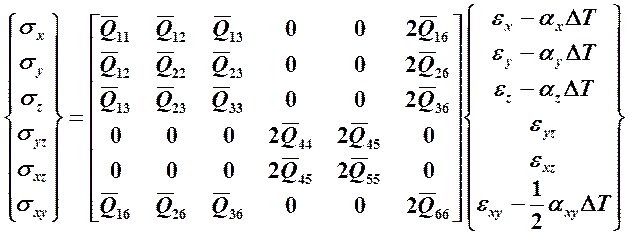     (18.11)

где , или в развёрнутой форме

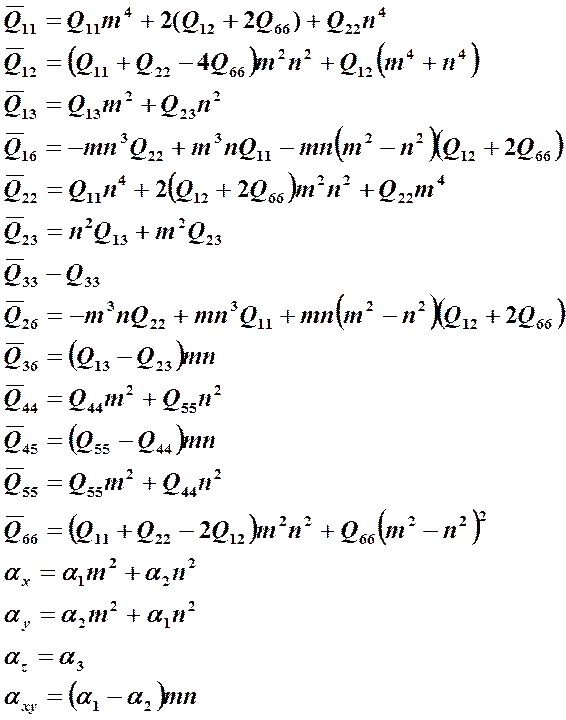(18.12)

Для предварительного анализа в осях х и у можно пользоваться записью:

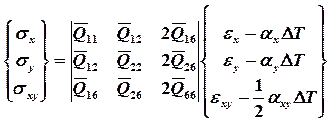
(18.13)

Для определения Q_ij  необходимо пользоваться (18.10).

19. Анализ многослойных композитных структур

Зависимости, рассмотренные в предыдущем разделе, относятся к одному слою композитного материала. В реальных конструкциях используется многочисленное количество слоев уложенных под различными углами друг к другу, вследствие чего можно изменять характеристики прочности и жесткости в зависимости от направления действия сил.

Рассмотрим слоистый материал, образованный n слоями.

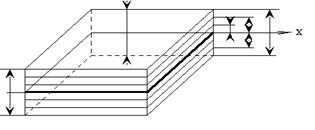
Рис. 19.1 Обозначение последовательности укладки слоёв.

Для  k – го слоя уравнение имеет вид:

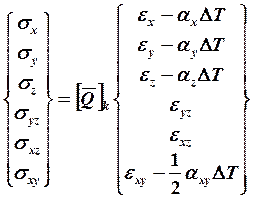                                         (19.1)

В этом выражении все члены матрицы должны иметь индекс k и соответствовать расположению данного слоя пластины в координатах x-y.

Из выражения (19.1) видно, что если все величины входящие в его правую часть известны, то можно вычислить напряжения любого k-го слоя пластины. Рассмотрим слоистую пластину толщиной h (рис. 19.1)

h_k – расстояние от срединной плоскости (z = 0) до верхней поверхности k-го слоя. Для слоев лежащих ниже срединной поверхности эта величина является отрицательной, а для слоев лежащих выше этой плоскости – положительной.

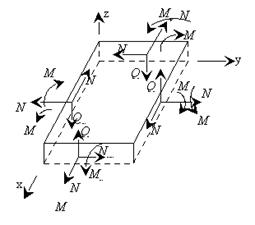
Введем нормальные усилия N, изгибающие моменты M и поперечные усилия Q для всей пластины в целом (рис. 19.2).   

Уравнения равновесия для этой пластины выглядят следующим образом:

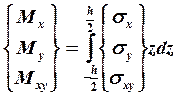;        (19.2)

Рис. 19.2 Нормальные усилия, изгибающие моменты и поперечные усилия для пластины в целом.

Подставив в (19.2) значения напряжений согласно (19.1), а также с учетом того, что перемещения срединной поверхности, углы поворота, а также коэффициенты Q не являются функциями z, получим:

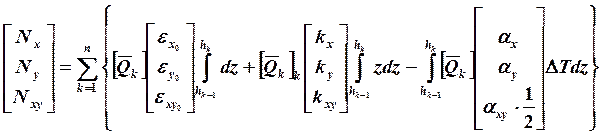           (19.3)

Или же в компактном виде:

                                   (19.4)

где:

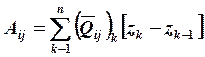                                                     (19.5)

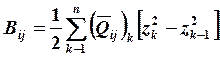                                                 (19.6)

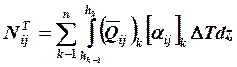                                             (19.7)

После интегрирования и подстановки напряжений получим:

                                                         (19.8)

здесь:

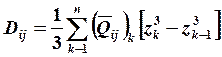                                                                (19.9)

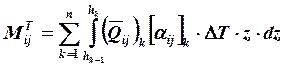                                                   (19.10)

где  ij = 1,  2,  6.

Для определения поперечных усилий Q_x и Q_y, принимается, что поперечные касательные напряжения распределены по параболическому закону по толщине слоистой стенки

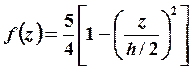                                                     (19.11)

тогда:

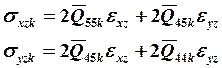                                               (19.12)

или

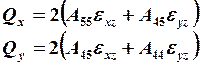                                                  (19.13)

здесь:

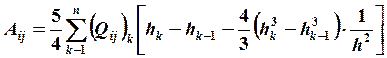                                 (19.14)

ij = 4,  5.

Окончательно (19.4)  и  (19.8) могут быть записаны:

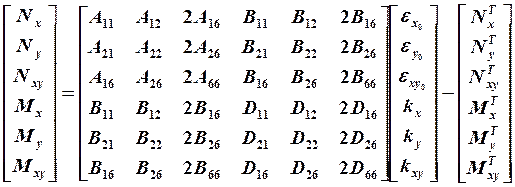                     (19.15)

Из выражения (19.15) видно, что подматрица [А] является матрицей мембранных жесткостей, связывающей усилия N и деформации срединной поверхности. Подматрица [D] является матрицей изгибных жесткостей, которая связывает изгибающие моменты и привязку k. Подматрица [B] связывает изгибающие моменты М и деформации срединной поверхности, а также N и k. Эта подматрица называется матрицей смешанных жесткостей. В случае, когда укладка пластины имеет симметричную структуру, коэффициенты  Связь между растяжением и сдвигом имеет место в случае, если А₁₆ и А₂₆ не равны нулю. Связь кручения с растяжением, а также изгиба со сдвигом имеет место при нулевых В₁₆ и В₂₆, а связь изгиба с кручением характеризуется отличными от нуля величинами D₁₆ и D₂₆.