Композиты относятся к анизотропным материалам, т.е. к материалам, характеристики которых зависят от направления, в отличие от изотропных которые характеризуются одинаковыми механическими, физическими, температурными и электрическими свойствами в любом направлении. Понятие изотропии материала является условным и определяет по существу лишь математическую модель реального материала. Например, в поликристаллических металлах, состоящих из многочисленных анизотропных зерен, макроскопическая изотропия является следствием случайного распределения отдельных, случайно ориентированных зерен. В то же время некоторые материалы могут быть макроскопически анизотропными благодаря структуре, образующейся в процессе технологических операций (ковка, вытяжка). Другие материалы, так же как и древесина и все материалы, армированные волокнами, являются анизотропными по своей природе.
Композитные материалы, армированные волокнами, представляют исключительный интерес, поскольку использование длинных волокон обеспечивает материалу более высокое отношение прочности и жесткости к плотности. Кроме того, существует возможность направленного расположения волокон в соответствии с заданной геометрией изделия, приложенными нагрузками и условиями эксплуатации. Сочетание двух и более типов волокон с одной матрицей, например, использование более прочных и жестких волокон в сочетании с более дешевыми и, следовательно, с более пригодными для менее нагруженных участков конструкции, открывает новый класс материалов. Таким образом, при использовании композиционных материалов инженер не только выбирает материал, но и одновременно является и его создателем.
Рассмотрим упругое твердое тело произвольной формы и допустим оно образовано бесконечным множеством материальных точек. Из этого тела выделим элементарный параллелепипед со сторонами dx, dy и dz. Этот элемент отнесем к декартовой системе координат x, y, z (cм. рис.17.1).
 |
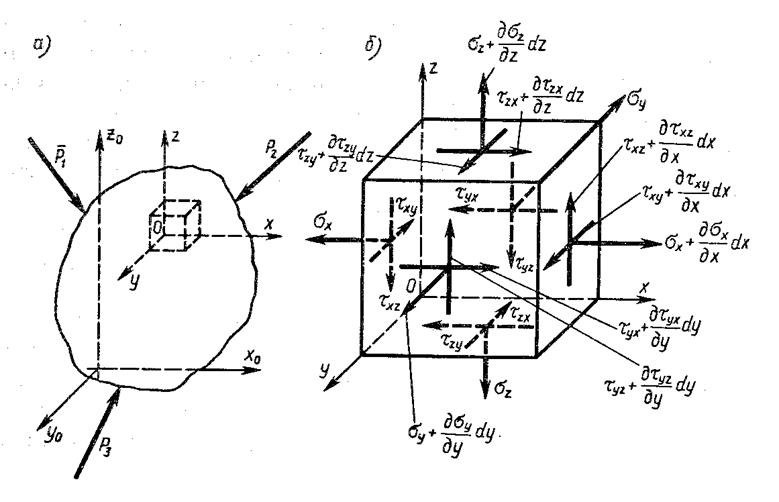Для напряжения, действующего на площадке, внешняя нормаль которого совпадает с положительным направлением оси, положительным является напряжение, направление которого совпадает с направлением оси. Когда напряжение действует на площадке, внешняя нормаль к которой совпадает с отрицательным направлением оси, напряжение положительно, если его направление совпадает с отрицательным направлением оси. Первый индекс любого напряжения, на любой площадке элементарного объема, обозначает ось, которой параллельна внешняя нормаль к площадке; второй индекс обозначает ось, которой параллельно напряжение.
Деформации, возникающие в упругом теле, имеют те же индексы, что и напряжения, но бывают двух типов. Линейные деформации обозначаются εij, где i = x, y, z и являются мерой изменения размера элементарного объема. Деформации сдвига γij пропорциональны отклонению углов элементарного объема ΔV под действием касательных напряжений τij. В качестве примера рассмотрим грань параллелепипеда в плоскости х – у (рис. 17.2).
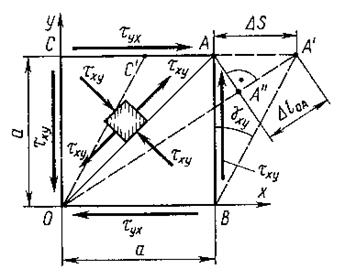
Рис. 17.2. Деформация элемента, испытывающего чистый сдвиг.
Касательные напряжения деформируют прямоугольный элемент в параллелограмм с углом при вершине φ. Изменение угла при вершине γху = π/2 – φ. Сдвиговые деформации являются тензорными величинами и определяются выражениям:
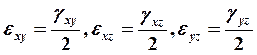(17.1).
Из курса сопротивления материалов, известно, что напряжения σij связаны с деформациями εij следующим уравнением:
(17.2)
где i, j, k, l принимают значения 1, 2, 3 или х, у, z в Декартовой системе координат.
Тензоры напряжений и деформаций являются симметричными, т. е. σij = σji, εkl = εlk.
Поэтому можно принять
σ11 = σ1 σ23 = σ4 ε11 = ε1 2ε23 = ε4
σ22 = σ2 σ31 = σ5 ε22 = ε2 2ε31 = ε5 (17.3)
σ33 = σ3 σ12 = σ6 ε33 = ε3 2ε12 = ε6
с учётом (17.3) равенство (17.2) можно записать
σ1 = с11ε1 + с12ε2 + с13ε3 + с14ε4 + с15ε5 + с16ε6
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.