Прочность конструкций. Деформации крыла от изгиба в плоскости хорд

Лекция № 11.    Прочность конструкций        семестр 6.    2009 г.

Определение прогибов

Так как при изгибе  предполагаем, что сечение крыла перемещается без закручивания, то изгиб крыла можно определить как прогиб любого продольного его элемента. Возьмем для этой цели основной лонжерон. Из формулы

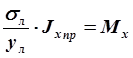;  ;    - статический момент, центробежный момент и момент инерции приведенных площадей сечения; из них имеем следующее:

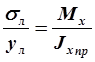, отметим, что J_{x np} – момент инерции п р и в е д е н н о г о   с е ч е н и я.

Разделив теперь правую и левую части на Е_л , получим:

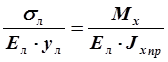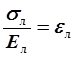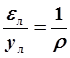.  Но  ;  ,  где   - кривизна оси балки.

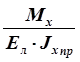Если нами произведен расчёт ряда сечений крыла, то мы можем построить кривую  по z или иначе    по z (см. рис. 2.28, а ).  Но 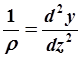 ,  следовательно, прогибы можно получить двойным интегрированием эпюры :

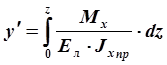, - (см. рис. 2.28. б); 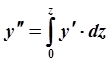      , (рис. 2.28, в).

При интегрировании следует сразу учесть краевые условия: при  z = 0, 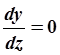 и у = 0.

Для этого достаточно интегрирование  эпюры производить от корня крыла к его концу, как указано стрелкой.

Таким образом, расчёт ведётся так же, как для обычной балки, но используется при этом момент инерции редуцированного, а не полного сечения.

При определении прогибов стреловидного крыла следует иметь ввиду, что стреловидная заделка внесёт некоторые поправки к найденным здесь прогибам.

Деформации крыла от изгиба в плоскости хорд обычно не определяются, так как они ничтожно малы.

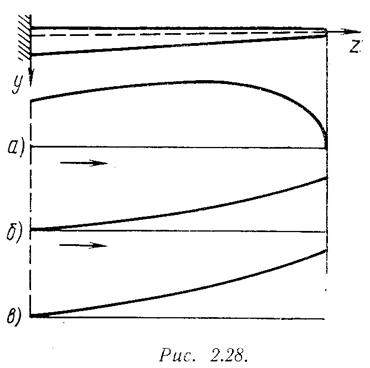
2.4. Депланация[1] поперечных сечений при сдвиге – кручении.  

Условие замкнутости контура. (Неполная часть…)

Расчёт крыла на изгиб производился, принимая во внимание только изгибающий момент в сечении. В конструкции крыла изгиб возникает от поперечной нагрузки, следовательно, в сечениях кроме изгибающего момента будут действовать также поперечные силы, которые в общем случае вызовут деформации сдвига сечения и закручивания.

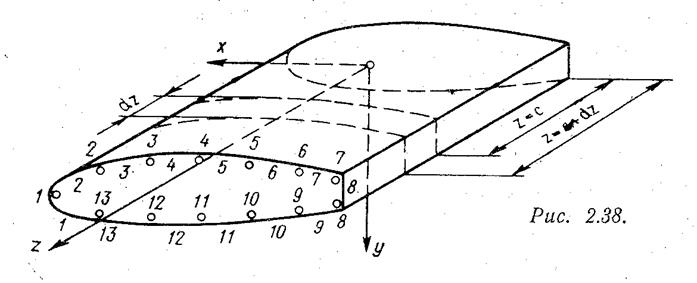
Раньше, чем перейти к рассмотрению методов расчёта тонкостенного крыла на сдвиг и кручение, остановимся на вопросах, связанных с качественной стороной характера деформаций при сдвиге – кручении. Рассмотрение этих вопросов даст возможность установить важные зависимости между смещениями точек сечения и касательными напряжениями, значительно облегчающие изложение и понимание всех дальнейших разделов расчёта тонкостенного крыла. Знание явлений, излагаемых в этом разделе, совершенно необходимо для понимания и исследования современных проблем тонкостенных конструкций.

В связи с этим, правда, несколько позже, мы всё равно не смогли бы пройти мимо этих явлений, но,  с нашей точки зрения, целесообразно ознакомиться с явлениями депланации сечений по возможности раньше.

В.Н. Беляев, разрабатывая методы расчёта тонкостенного крыла на свободные сдвиг и кручение, пользовался энергетическим методом. Таким образом, он оставлял в тени механическую сторону протекающих явлений и лишь при изучении стеснённого кручения был вынужден обратиться к явлениям депланации сечений.

Это создавало искуственный отрыв одной проблемы от другой, в то время как раннее ознакомление с депланацией сечений постепенно вводит читателя в круг проблем, связанных со стеснением деформаций. Одновременно изложение методов расчёта крыла на сдвиг и кручение становится более ясным,  освобождаясь от громоздких выражений потенциальной энергии.

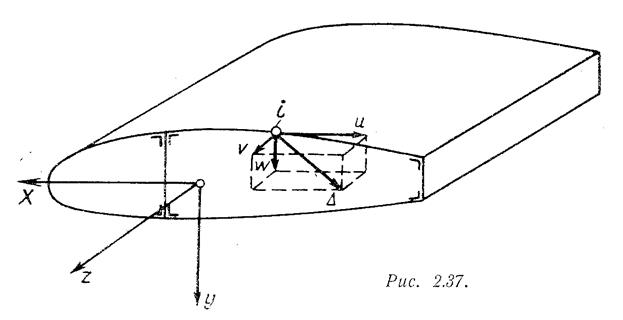
При расчёте конструкций мы обычно пользуемся методом нормальных сечений. Эти сечения получаем на ненагруженной конструкции, проводя соответствующие секущие плоскости. Таким образом, сечение конструкции, которое мы подвергаем дальнейшему исследованию, до деформации является плоским. В результате нагружения и деформации конструкции любая точка сечения i может получить какое-то пространственное перемещение Δ (рис. 2.37). Разложим это пространственное перемещение Δ на три составляющих:

u, w – перемещения в плоскости сечения по касательной и по нормали к контуру;

v – перемещение по нормали к сечению (по направлению к оси z).

При любых значениях перемещений u, w плоское до деформации сечение остаётся плоским. Перемещение же v выводит  точку i из плоскости сечения. Для того чтобы точки контура после деформации вновь оказались в одной плоскости, необходимо связать перемещения v одним законом – законом плоскости. В общем случае, очевидно,  перемещения  v ведут к короблению плоского до деформации сечения. В общем случае такое  сечение уже не будет плоским после нагружения конструкции. Перемещение точек поперечного сечения, преобразующее его в кривую поверхность или совокупность плоскостей, называется депланацией поперечного сечения.

Поэтому перемещение точек контура по направлению образующей цилиндра, приводящее к короблению его, будем в дальнейшем называть депланацией.