Прочность конструкций. Деформации крыла от изгиба в плоскости хорд, страница 2

Итак, осевые перемещения точек контура, как правило,  ведут к депланации сечения и только в очень частном случае, когда они подчинены закону плоскости, сечение после деформации остаётся плоским ( это имеет место, например, при чистом изгибе балки). Каковы же депланации сечений в общем случае нагружения крыла? Как связаны эти депланации с напряжениями в сечении? Эти вопросы получат некоторое освещение в данном разделе.

Рассмотрим крыло постоянного, но совершенно произвольного сечения с совершенно произвольным нагружением и краевыми условиями (рис. 2.38).

При рассмотрении будем опираться на гипотезу неизменности формы контура поперечного сечения, т. е. будем предполагать, что нервюры крыла столь жёстки в своей плоскости и так часто расставлены по длине крыла, что деформации сечений крыла в их плоскости пренебрежительно малы. Эта гипотеза, с соответствующими оговорками или без них, имеет всеобщее распространение и считается хорошо соответствующей действительной схеме явления.

Положим также, что касательные напряжения, возникающие в конструкции, постоянны по толщине обшивки и направлены по касательной к контуру. Кроме того, также, как это мы делали при расчёте крыла на изгиб, упростим несколько схему распределения нормальных напряжений по сечению, относя их только к продольным рёбрам (стрингеры и полки лонжеронов с присоединённой обшивкой).

Вырежем в конструкции крыла двумя параллельными сечениями z = c и z = c + dz отсек длиной dz (см. рис. 2.38).

Пронумеруем продольные рёбра панели  обшивки, обходя контур по часовой стрелке, как это показано на рис 2.38. Если какая-либо точка i сечения z = c в результате деформаций получает перемещения  u, v  и  w, то соответствующая точка в сечении z = c+ dz  сместится уже на                                                     

 

;                             ;                            .

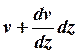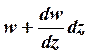Следовательно, если мы  будем  использовать не полные смещения, а смещения относительно сечения z = c, то эти смещения соответственно будут равны:

;                            ;                        .

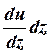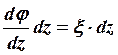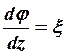Перемещения в плоскости данного сечения  u,  w  связаны принятой нами гипотезой о неизменности формы контура поперечного сечения.

Известно, что любое перемещение жёсткого диска в своей плоскости может быть заменено  вращением относительно некоторой неподвижной точки.

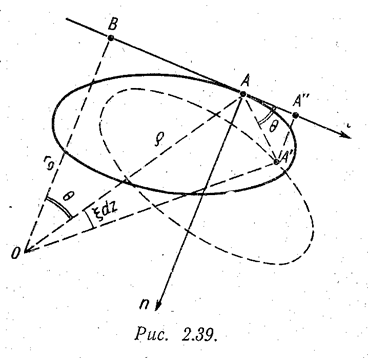
На рис. 2.39 изображены два положения сечения: исходное и положение в результате смещений в своей плоскости.

Точка О и есть тот мгновенный центр, одним вращением относительно которого сечение из первого положения может быть переведено во второе. Некоторая точка А сечения переместится тогда в положение А΄, описав дугу окружности радиусом  ρ.

Угол между начальным и конечным положением радиуса будет, очевидно, равен

.

Здесь φ – угол закручивания конструкции;

- (кси) – относительный угол закручивания.

Постоим в точке А касательную t  и нормаль n к контуру и разложим перемещение АÁ

 

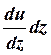по этим направлениям. Отрезок АА´´, очевидно, даст нам            . Легко видеть, что

АА΄ = ρξdz;            АА´´= АА´соs θ.

Следовательно,

                                  

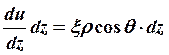
Опустим теперь из точки О  перпендикуляр на касательную t(OB). Нетрудно видеть, что угол АОВ равен углу А΄АА΄΄, следовательно, длина построенного перпендикуляра равна

     

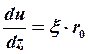
, откуда                                                           (2.24)

свяжем теперь полученное перемещение по направлению касательной к контуру  u с перемещением по нормали к сечению  v  ( с осевым перемещением, ведущим к депланации).

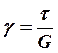В обшивке конструкции в общем случае будут действовать какие-то касательные напряжения  τ , вызывая деформации сдвига. Относительный угол сдвига γ, очевидно, может быть записан так:

.                                              (2.25)

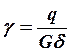Поскольку мы считаем, что   τ  не меняется по толщине обшивки, нам удобнее записать эту формулу, перейдя от напряжения к погонному касательному усилию q = τ δ. Умножим для этого числитель и знаменатель правой части равенства (2.25) на δ (толщину обшивки); тогда

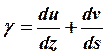                                                                                                       (2.26)

Но, с другой стороны.                   

,             (2.27)

где s – криволинейная координата точки по контуру сечения.