Расходы на содержание СП превышает 15%.
В среднем уровень механизации составляет 15%, оббьем работ по СП равен 18%
Теория вероятности.
Основные определения теории вероятности.
В некоторых случаях вероятность какого то события не очевидна и поэтому необходимо устанавливать относительную вероятность наступления какого либо события. Любое промежуточное значение между нулем и 1 является относительной вероятностной мерой.
Априорная вероятность – это такой тип вероятности который может быть определен из самой природы события.
Частота = число благоприятных исходов / общее число событий
При увеличении числа опытов до бесконечности данное отношение стремиться к некоторому пределу – этот придел и называется вероятностью события.
Функция распределения позволяют находить вероятности случайных событий связанных с данными случайными величинами.
Математическое ожидание (среднее значение)
Математическое ожидание не дает информацию о возможных отклонениях случайной величины от того или иного значения. Математическое ожидание может дать информацию о величине погрешности.
Числовые характеристики, которые отображают разброс значения случайной величины, называют характеристиками рассеивания.
Для того чтобы охарактеризовать разброс случайной величины. Рассматривают отклонение X-mx
X – случайная величина
Если эта разница отрицательна то рассматривают ее модуль либо квадрат.
Дисперсия случайной величины назвываеться математическое ожидание квадрата ее отклонения от математического ожидания
Сумма вероятностей наступления события и вероятности не наступления события всегда равна 1.
Вероятность безотказной работы:
U – вероятность отказа отдельного элемента
К – количество параллельно соединенных элементов
На практике рассматриваются следующие вопросы
1. Насколько велики отклонения значений фактически принимаемых данной случайной величиной от ее среднего значения.
2. Будут ли эти значения побольше части тесно сгрупированны от среднего значения или он будут рассеяны и значительно отличаться от среднего значения.
Нормальное распределение плотности вероятности случайной величины.
Нормальный закон описывает распределение случайной влечены которая группируется около среднего значения и появляется с определенной частотой.
Кривая описывающая нормальный закон или кривая описывающая частоты имеет колокола образную форму и называется кривая распределения. Распределение возникает тогда когда на исследуемую величину действует система многих случайных факторов каждый из этих факторов незначительно действует.
Размах распределения зависит от вызвавший его системы факторов
Если число интервалов увеличивается то ширина их пропорционально уменьшается ток что кривая приближается с кривой нормального распределения.
Формула кривой:
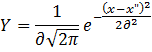
Правило 3х сигм
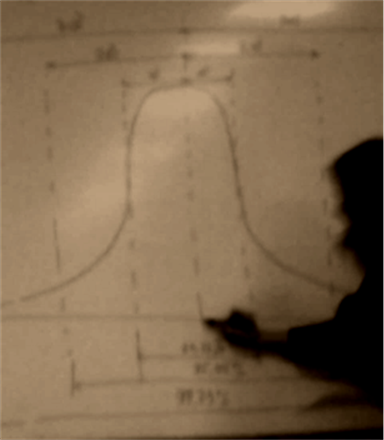
Среднее квадратическое отклонение равно 1/6 размаха кривой.
Особенности нормального распределения:
1. Все кривые нормального распределении имеют 1 наивысшую точку при удалении, от которой в право и в лево эти кривые снижаются. (при удалении значения случайной величины от ее наивероятнейшего значения, вероятности убывают)
2. Все кривые нормального распределения имеют одинаковую форму. Они могут различаться по 2м параметрам:
a. По среднему значению
b. По среднему квадратическому отклонению
3. Площади под кривыми нормального распределения равны 1
Экспонинцеальный закон распределения специальных отказов.
Описывает появление событий имеющих 2 исхода взаимно исключающих друг друга.
В ПХ этот закон может быть использован для прогнозирования вероятности безотказной работы детали, изделия или элемента во времени.
Среднее число отказов за время Т. λТ
λT
- вероятность отсутствия отказов за время Т
λT
Вероятность 1го отказа за время Т
В самом простом случае Р(t)= в этом случае интенсивность отказа
выражается в единицах обратных единицы времени. Надежность это вероятность того
что устройство с постоянной интенсивностью отказов не откажет в течении
заданного времени.
Период работы для которого справедлива данная формула это период нормальной эксплуатации.
Параметры потока отказов
Параметр плотности распределения отказов определяет надежность устройств. Среденяя наработка на отказ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.