Уравнение Кортевега-де Фриза, страница 2

Первая задача может иметь решения лишь при . При этом решения  при , асимптотику следующего вида

Предположим, что обе задачи решены и определены совокупности и . Эти данные принято называть данными рассеяния.

Пусть нам известно данные рассеяния для некоторого потенциала. Поставим задачу нахождения по данным рассеяния соответствующего потенциала.

По данным рассеяния строится функция

Эта функция называется ядром уравнения Гельфанда-Левитана, а затем ищется ядро следующего линейного интегрального уравнения.

(3)

Решив уравнение Гельфанда-Левитана по формуле

 (4)

определяем , которая является искомым потенциалом.

Схема метода

Рассмотрим задачу Коши для уравнения (1).

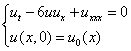
Решение задачи Коши назовём быстроубывающим, если  и все её производные до третьего порядка включительно являются быстро убывающими функциями.

Теорема 1. Если потенциал  является быстроубывающим решением уравнения КДФ, то собственные значения  не зависит от времени .

Теорема 2. Если потенциал  является быстроубывающим решением уравнения КДФ, то данные рассеяния  зависят от времени следующим образом

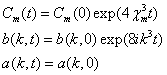    (5)

Таким образом мы приходим к следующей схеме отыскания быстроубывающих решений.

Рассматривая уравнение