Расчет допусков в приборостроении. Основные определения, страница 4

Номинальный диаметр сопряжения 80мм, допустимая несоосность не должна превышать e=30 мкм,

Необходимо определить допуски составляющих размеров методом равных допусков.

Так как несоосность равна половине зазора , то наибольший зазор равен удвоенной несоосности , следовательно,

 

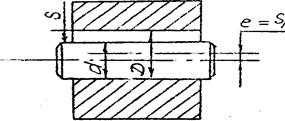
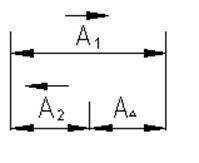
Рис. 2.2. Подшипник скольжениия и его размерная цепь.

= 60 - 10= 50 мкм.

По формуле (2.9) поучаем

= 50/2 = 25 мкм, где m= 3.

Допуск для деталей 6-го квалитета равен 19 мкм, для 7-го квалитета - 30 мкм. Так как в системе отверстия обычно применяют сопряжения отверстия 7-го квалитета с валами 6-го квалитета, то, приняв

= 30мкм, а = 19 мкм, получим

= 30 + 19 = 49 мкм, что удовлетворяет условию задачи.

2.2.3. Метод максимума - минимума

Этот метод чаще применяют при индивидуальном и мелкосерийном производстве изделий, при проектировании единичных устройств, приспособлений :

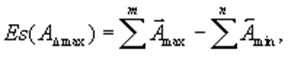  (2.11)

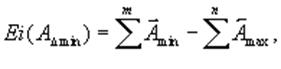  (2.12)

Допуск замыкающего звена

(2.13)

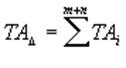(2.14)

Из соотношения (2.14) можно заключить, что при использовании методов полной взаимозаменяемости повышения точности замыкающего звена можно добиться :   1) уменьшением допусков каждого из составляющих звеньев ;

  2) сокращением числа звеньев размерной цепи.

Расчеты размерных цепей по методу максимума-минимума фактически сводятся к ранее рассмотренным методам равного квалитета (см. пример I) и равных допусков .

2.3 Методы неполной взаимозаменяемости

Методы неполной взаимозаменяемости (теоретико-вероятностные методы) нашли широкое применение, особенно при большом числе эвеньев, входящих в размерную цепь. В настоящее время существует значительное количество вероятностных методов: равных допусков, равного квалитета, пропорционального влияния, максимального числа единиц допуска и др. Использование того или иного метода на стадии проектирования, когда информация о будущем изделии сравнительно мала, зависит от количества и качества имеющейся априорной информации. Ниже рассмотрены лишь те вероятностные методы, которые требуют минимальной исходной информации о законах распределения производственньгх погрешностей в звеньях изделия.

Методы неполной взаимозаменяемости, основанные на вероятностных методах суммирования допусков, позволяют получить допуски на составляющие звенья размерной цепи при методе равных допусков по формуле (2.15), а при методе равных квалитотов точности по формуле (2.16), по которой определяют число единиц точности "а" и далее находят квалитет

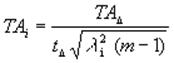, (2.15)

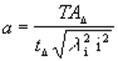, (2.16)

где

- коэффициент риска, выбираемый в зависимости от принятой вероятности риска р выхода величины за пределыдопуска по табл.2.4

- коэффициент формы кривых, характеризующих закон распределения производственных погрешностей в звеньях;

- когда ничего не известно о характере закона распределения (закон равной вероятности), что соответствует расчёту размерных цепей изделий мелкосерийного и единичного производства;

- когда закон распределения близок к закону Симпсона (закону треугольника) ;

- когда закон распределйния является нормальным (закон Гаycсa), используется при расчете размерных цепейизделий массового производства;

m - Число звеньев размерной цепи.

Значение коэффициентов риска

Таблица 2.4

Риск р , %	32	10	4,5	1,0	0,27	0,1	0,01
	1	1,65	2	2,57	3	3,29	3,89

Использование вероятностных методов рассмотрим на примерах.

Пример 3.