Для прямозубой зубчатой пары принимаем следующие материалы:
- шестерня –
сталь 40Х с термической обработкой поверхностная закалка до твердости HRC 45-50, ![]() =920МПа,
=920МПа, ![]() =790МПа;
=790МПа;
- зубчатое колесо – сталь 45
улучшенная до твердости HB 180-350, ![]() =790МПа,
=790МПа, ![]() =640МПа.
=640МПа.
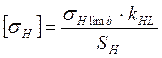 ,
,
где![]() -предел
контактной выносливости,
-предел
контактной выносливости,
-
для шестерни ![]()
![]() :
:
![]() =17*
=17*![]() +200=17*47,5+200=1007,5
МПа;
+200=17*47,5+200=1007,5
МПа;
-
для колеса (![]() =264,5):
=264,5): ![]() =2*HB+70=2*264,5+70=599МПа;
=2*HB+70=2*264,5+70=599МПа;
SH-коэффициент безопасности,
- для шестерни SH=1,2;
- для колеса SH=1,1.
kHL – коэффициент долговечности,![]() ,
,
где![]() базовое
число циклов перемены напряжений,
базовое
число циклов перемены напряжений,
-
для шестерни ![]() ==90*106;
==90*106;
- для колеса =15*106.
![]() расчетное число циклов переменных напряжений,
расчетное число циклов переменных напряжений,
- для шестерни:
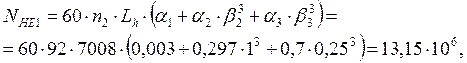
- для колеса:
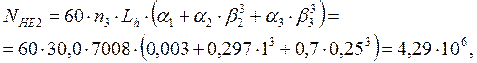
где ![]() -
параметры режима нагружения (по графику);
-
параметры режима нагружения (по графику);
![]()
![]()
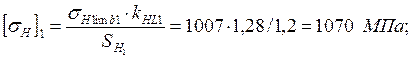
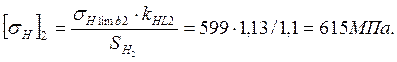
При кратковременных перегрузках максимальное допускаемое контактное напряжение:
-
для шестерни: ![]() ;
;
-
для колеса: ![]() .
.
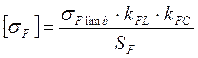 ,
,
где![]() -
предел контактной выносливости,
-
предел контактной выносливости,
-
для шестерни ![]()
-
для колеса ![]() =1,8
=1,8![]() =1,8*265=477 МПа;
=1,8*265=477 МПа;
SF - коэффициент безопасности,
- для шестерни SF1=1,75-2,1, принимаем SF1=1,95;
- для колеса SF2=1,75-2,0, принимаем SF2=1,95;
kFC - коэффициент, учитывающий влияние двустороннего приложения нагрузки, для нереверсивных передач kFC=1,0;
kFL – коэффициент долговечности,![]() ,
,
где ![]() базовое число циклов переменных
напряжений, для всех сталей NF0=4*106;
базовое число циклов переменных
напряжений, для всех сталей NF0=4*106;
![]() - расчетное число циклов
переменных напряжений,
- расчетное число циклов
переменных напряжений,
-
для шестерни![]() =
=![]() =13,15*106;
=13,15*106;
-
для колеса ![]() =
=![]() =4,29*106;
=4,29*106;
![]() ,
,
принимаем kFL1=1,0.
![]() .
.
принимаем kFL2=1,0
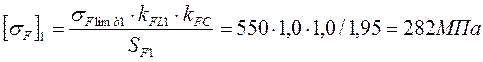 ;
;
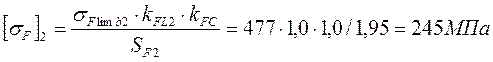 .
.
При кратковременных перегрузках максимальное допускаемое изгибное напряжение:
-
для шестерни ![]() ;
;
-
для колеса ![]() .
.
-
. Межосевое расстояние из условия допустимой контактной выносливости:
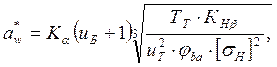
где ![]() – коэффициент,
учитывающий неравномерность распределения нагрузки по ширине венца [табл. 3.5;
стр. 39; 4].
– коэффициент,
учитывающий неравномерность распределения нагрузки по ширине венца [табл. 3.5;
стр. 39; 4].
![]() – числовой
коэффициент для косозубой передачи;
– числовой
коэффициент для косозубой передачи;
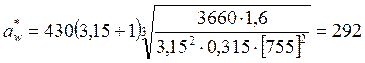 мм
мм
В соответствии с ГОСТ 2185-81 принимаем значение
межосевого расстояния ![]() мм.
мм.
Определение модуля:
![]()
В соответствии с ГОСТ 6636-69 принимаем значения
модуля ![]() .
.
Расчёт количества зубьев колеса и шестерни при
угле наклона зубьев ![]() :
:
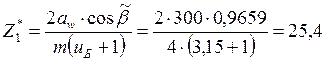
![]()
Конструктивно принимаем значение числа зубьев
колеса и шестерни ![]()
Определение фактического передаточного числа быстроходной передачи:
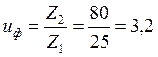
X1 = 0 и X2 = 0по рекомендации ГОСТ 13375-81 и ![]() .
.
Определение истинного угла наклона зубьев:
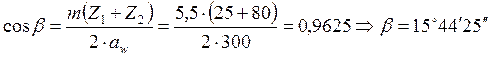
Определение начальных и делительных диаметров при
![]() и
и ![]() :
:
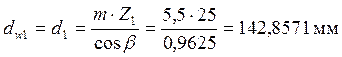
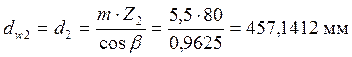
Определение диаметров вершин:
![]()
![]()
Определение диаметров впадин:
![]()
![]()
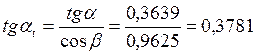 ,
,
где ![]() – угол профиля в
торцевом сечении.
– угол профиля в
торцевом сечении.
Определение ширины зубчатого венца:
![]()
В соответствии с ГОСТ 6636-69 ![]() 90
90
Определение высоты зуба колеса:
h = 2,5m = 2,5 × 5,5 = 13,75 мм.
Окружная скорость:
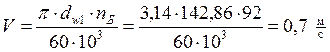
Окружная сила:
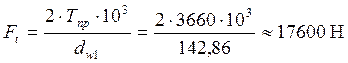
Осевая сила:
![]()
Радиальная сила:
![]()
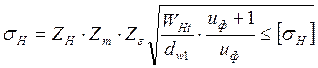 ,
,
где ![]() – коэффициент,
учитывающий форму сопряжения поверхности зубьев;
– коэффициент,
учитывающий форму сопряжения поверхности зубьев;
![]() , для стальных
колёс – коэффициент, учитывающий механические свойства материала сопряжённых
колёс;
, для стальных
колёс – коэффициент, учитывающий механические свойства материала сопряжённых
колёс;
![]() – коэффициент,
учитывающий суммарную длину контактных линий.
– коэффициент,
учитывающий суммарную длину контактных линий.
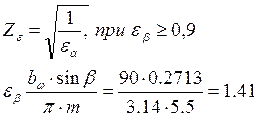
где ![]() – коэффициент
торцевого перекрытия.
– коэффициент
торцевого перекрытия.
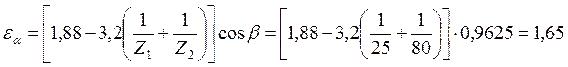
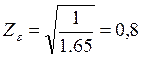
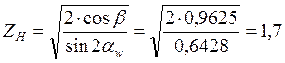
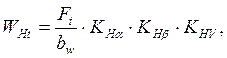
где ![]() – коэффициент,
учитывающий распределение нагрузки[табл. 3.4; стр. 39; 4];
– коэффициент,
учитывающий распределение нагрузки[табл. 3.4; стр. 39; 4];
![]() – коэффициент,
учитывающий неравномерность распределения нагрузки по ширине венца[табл. 3.5;
стр. 39; 4].
– коэффициент,
учитывающий неравномерность распределения нагрузки по ширине венца[табл. 3.5;
стр. 39; 4].
![]() [табл. 3.6; стр. 40; 4]
[табл. 3.6; стр. 40; 4]
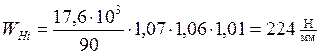
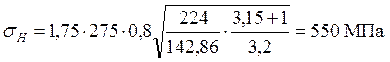
Так как разность между ![]() и
и
![]() не превышает 10 процентов, быстроходная
передача по условию контактной выносливости рассчитана верно.
не превышает 10 процентов, быстроходная
передача по условию контактной выносливости рассчитана верно.
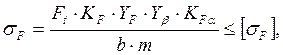
где ![]() – коэффициент,
учитывающий форму зуба [стр. 42; 4];
– коэффициент,
учитывающий форму зуба [стр. 42; 4];
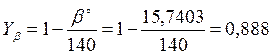 – коэффициент,
введённый для компенсации погрешности;
– коэффициент,
введённый для компенсации погрешности;
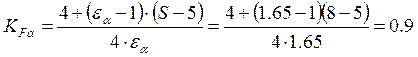 – коэффициент,
учитывающий неравномерность распределения нагрузки между зубьями;
– коэффициент,
учитывающий неравномерность распределения нагрузки между зубьями;
![]()
S – степень точности;
![]() –
коэффициент нагрузки,
–
коэффициент нагрузки,
где ![]() – коэффициент,
учитывающий неравномерность распределения нагрузки по длине зуба [табл. 3.7;
стр. 43; 4];
– коэффициент,
учитывающий неравномерность распределения нагрузки по длине зуба [табл. 3.7;
стр. 43; 4];
![]() – коэффициент,
учитывающий действие динамической нагрузки [табл. 3.8; стр. 43; 4].
– коэффициент,
учитывающий действие динамической нагрузки [табл. 3.8; стр. 43; 4].
![]()
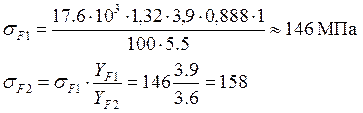
Так как ![]() передача
по напряжению изгиба рассчитана, верно.
передача
по напряжению изгиба рассчитана, верно.
|
|
z1=25 |
z2=80 |
aW=300,0 мм |
|
d1= dW1=142,86 мм |
d2= dW2=457.14 мм |
da1=153.86 мм |
da2=468.14 мм |
|
df1=131.86 мм |
df2=446.14 мм |
V=0,7 м/c |
|
|
bW1=100,0 мм |
bW2=90,0 мм |
U2=3.15 |
UФ=3.2 |
|
Ft=17600 H |
FR=6450 H |
Fx=3375 |
х=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Расчет конической передачи
5.1 Выбор материала конического колеса и шестерни, расчёт
допускаемых напряжений изгиба
Для изготовления
конического колеса и шестерни выбираем сталь 40Х (HRC=45-55, ![]() ); вид ТО – поверхностная закалка.
); вид ТО – поверхностная закалка.
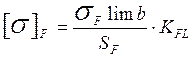 ,
,
где ![]() предел изгибной выносливости при
базовом числе циклов; SF – коэффициент безопасности; КFL –коэффициент долговечности рассчитывается с учетом
базового числа нагружения NF0,
предел изгибной выносливости при
базовом числе циклов; SF – коэффициент безопасности; КFL –коэффициент долговечности рассчитывается с учетом
базового числа нагружения NF0,
![]() 1=
1=![]() 2=550 МПа;
2=550 МПа;
SF =1,75 – для проката;
NF01= NF02=4×106- для сталей
Коэффициент
эквивалентности нагрузки при расчете на изгибную прочность: ![]() (при HB>350);
(при HB>350);
Расчетное число циклов для напряжений изгиба:
![]() циклов,
циклов,
![]() =1,
т.к. NFO1,2 < NFE 1,2.
=1,
т.к. NFO1,2 < NFE 1,2.
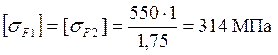 .
.
5.2 Определение нормального модуля конической передачи 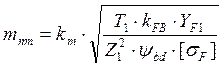
где ![]() =1,47 - коэффициент, учитывающий
распределение нагрузки по ширине венца по табл. 7.2[4],
=1,47 - коэффициент, учитывающий
распределение нагрузки по ширине венца по табл. 7.2[4],
![]() =14,5 – вспомогательный коэффициент,
=14,5 – вспомогательный коэффициент,
![]() = 17 – число зубьев шестерни
(задаемся),
= 17 – число зубьев шестерни
(задаемся),
![]() = 4,28 – эквивалентное число зубьев
по табл. 1.23[4]
= 4,28 – эквивалентное число зубьев
по табл. 1.23[4]
![]()
![]() -
коэффициент ширины венца шестерни относительно среднего делительного диаметра,
-
коэффициент ширины венца шестерни относительно среднего делительного диаметра,
где ![]() - угол делительного конуса шестерни:
- угол делительного конуса шестерни:
![]() мм,
мм,
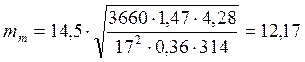 мм,
мм,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.