Работа №4. Моделирование распределения деформаций в массивных длинных образцах горной породы
I. Цель работы:
Научиться применять уравнения равновесия для определения распределения деформаций в длинных образцах горных пород, находящихся под действием поля силы тяжести.
Определить деформацию массивного образца из гранита цилиндрической формы, стоящего вертикально в поле силы тяжести. Длина образца l = 50 м, радиус r = 1 м, плотность r = 2500 кг/м3. Модуль Юнга E = 0,6 ГПа, коэффициент Пуассона n = 0,25. Построить графики деформаций ux, uy, uz от координат (x, y, z).
1. Используя функцию Matlab - int, определить явный вид выражений для деформаций.
Условие равновесия образца можно записать в следующем виде
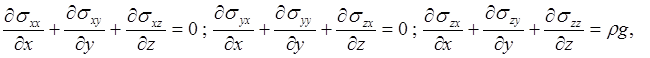
где sij - компоненты тензора напряжений. Исходя из граничных условий, на боковой поверхности образца компоненты тензора напряжений обращаются в нуль, кроме szz. На верхнем основании z = l, szz = 0.
Таким образом, решение уравнений равновесия есть
![]() , а остальные компоненты тождественно
равны нулю.
, а остальные компоненты тождественно
равны нулю.
Деформации можно получить интегрированием
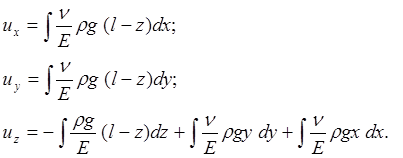
2. Построить трехмерные графики зависимостей деформаций от двух координат.
III. Пример оформления
Символьное интегрирование
» syms nu E po g l z x
» int('nu/E*po*g*(l-z)',x)
ans =
nu/E*po*g*(l-z)*x
Пример файла сценария, содержащего текст программы построения трехмерного графика
x = 0:0.1:1;
z = 0:5:50;
nu = 0.25; l = 50;
po = 2500; E = 0.6e9; g = 9.8;
[X,Z] = meshgrid(x,z);
Ux = -nu/E*po*g*X.*(Z-l);
hS1 = mesh(X,Z,Ux);
xlabel('Радиальная координата, м');
ylabel('Осевая координата, м');
zlabel('Деформация')
Пример графика деформации Ux
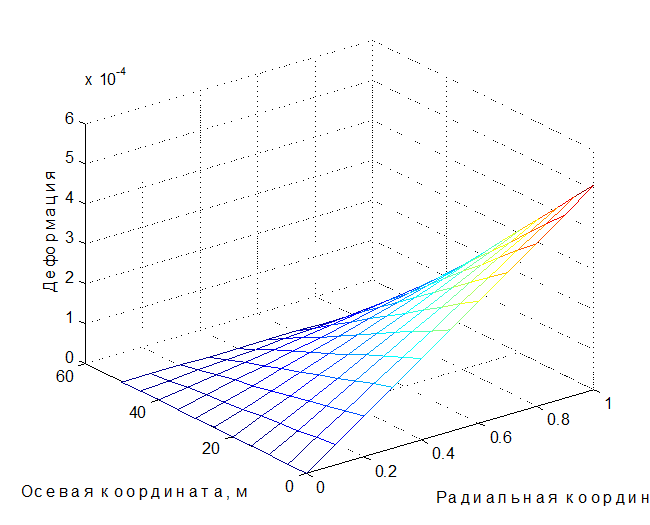 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.