


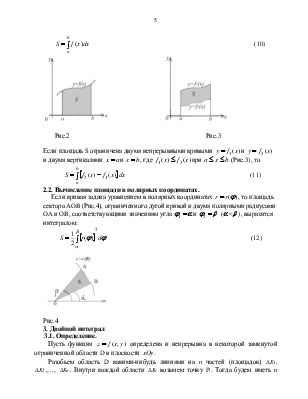















Криволинейный интеграл от
непрерывной в некоторой области плоскости ![]() функции
функции
![]() по координате
по координате ![]() вдоль
дуги плоской кусочно-гладкой кривой
вдоль
дуги плоской кусочно-гладкой кривой ![]() , расположенной в этой
области, связан с рассмотренным в пункте 4.1. криволинейным интегралом по длине
дуги соотношением
, расположенной в этой
области, связан с рассмотренным в пункте 4.1. криволинейным интегралом по длине
дуги соотношением
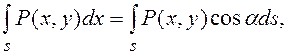
где ![]() -
угол между касательной, проведенной к кривой в любой ее точке, и положительным
направлением оси
-
угол между касательной, проведенной к кривой в любой ее точке, и положительным
направлением оси ![]() . Аналогично,
. Аналогично,
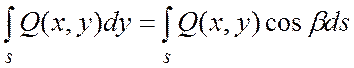 , где
, где ![]() -
угол между касательной, проведенной к кривой в любой ее точке, и положительным
направлением оси
-
угол между касательной, проведенной к кривой в любой ее точке, и положительным
направлением оси ![]() . Очевидно, что
. Очевидно, что 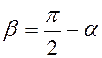 и
и ![]() .
.
Обычно рассматривают сумму
интегралов по координате ![]() и по координате
и по координате ![]() , которая записывается в виде
, которая записывается в виде
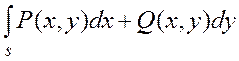 (22)
(22)
Криволинейные интегралы по координатам обладают теми же простейшими свойствами, что и интегралы по длине дуги. Однако в отличие от последних они зависят от выбора направления обхода кривой: если изменить направление обхода кривой, то интеграл (22) меняет знак, то есть
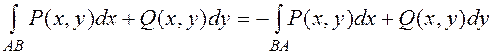
Для вычисления интеграла (22) пользуются одной из следующих формул:
a). если кривая задана уравнением ![]() и при перемещении из точки А в точку В
и при перемещении из точки А в точку В ![]() меняется от
меняется от ![]() до
до ![]() , то
, то
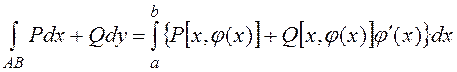 ; (23)
; (23)
b). если кривая задана уравнениями ![]() и при перемещении из точки А в точку В
параметр
и при перемещении из точки А в точку В
параметр ![]() меняется
от
меняется
от ![]() до
до ![]() , то
, то
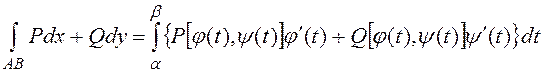 . (24)
. (24)
Замечание. В случае замкнутой кривой условимся брать направление
обхода кривой ![]() так, чтобы область, ограниченная
этой кривой, всегда оставалась слева.
так, чтобы область, ограниченная
этой кривой, всегда оставалась слева.
Аналогично определяются
криволинейные интегралы по координатам в случае, если кривая ![]() лежит в плоскости
лежит в плоскости ![]() или
или
![]() и от
непрерывных в некоторой пространственной области функций
и от
непрерывных в некоторой пространственной области функций ![]() вдоль дуги пространственной кусочно-гладкой
кривой
вдоль дуги пространственной кусочно-гладкой
кривой ![]() , расположенной в этой области, то есть
, расположенной в этой области, то есть
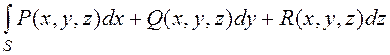 .
.
Если кривая задана параметрическим уравнением
![]()
![]() , то
, то
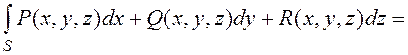
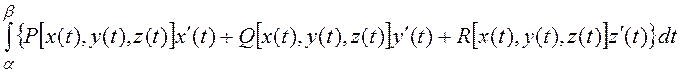 (25)
(25)
4.3. Приложения криволинейных интегралов (вычисление работы силы).
Пусть ![]() есть переменная сила, совершающая работу
есть переменная сила, совершающая работу ![]() вдоль пути
вдоль пути ![]() , и
функции
, и
функции ![]() и
и ![]() непрерывны
на кривой
непрерывны
на кривой ![]() ; тогда
; тогда
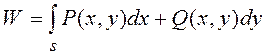 . (26)
. (26)
II. Пример выполнения контрольной работы.
1. Задание 361-370.
Дано
комплексное число 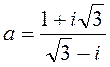 .
.
Требуется:
а) записать данное число в алгебраической, тригонометрической и показательной формах;
б) изобразить aна комплексной плоскости;
в)
вычислить ![]()
г)
найти все корни уравнения ![]() ;
;
д) вычислить произведение полученных корней;
е) составить квадратное уравнение с действительными коэффициентами, корнем которого является a.
Решение.
а) Используем формулу (3)
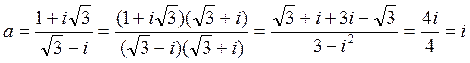
Получили чисто мнимое число a=0+i в алгебраической форме.
Вычислим модуль и аргумент полученного числа. По формулам (4) и (5):
![]()
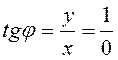
![]() - не существует, но (
- не существует, но (![]() ), следовательно
), следовательно 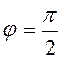 .
.
По формуле (6) запишем тригонометрическую форму числа a:
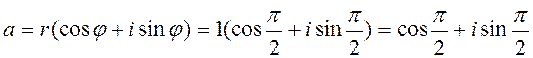
и по формуле (9) в показательной форме:
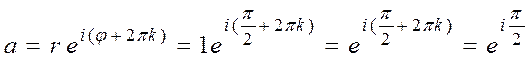
б) Изобразим число a=0+iна комплексной плоскости (Рис.5).
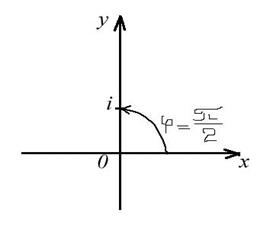
Рис.5
в)
вычислим ![]() по формуле (7):
по формуле (7):
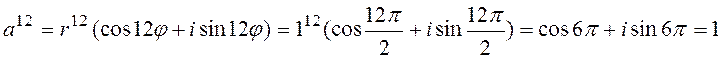
г)
найдем все корни уравнения ![]() :
:
![]() . Найдем все корни используя формулу (8):
. Найдем все корни используя формулу (8):
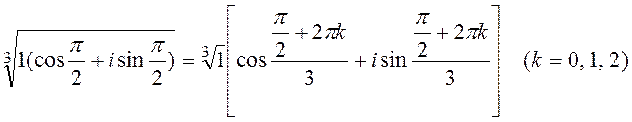
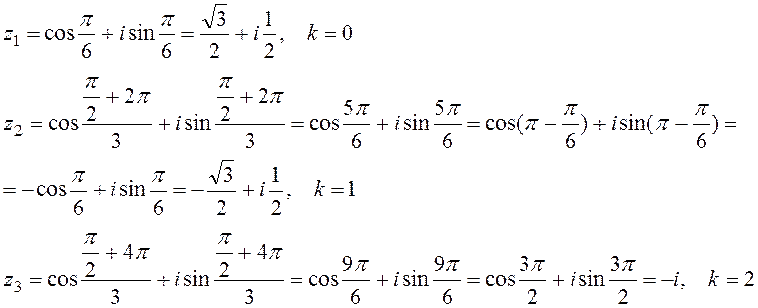
д) вычислим произведение полученных корней:
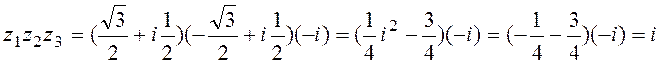
е) составим квадратное уравнение с действительными коэффициентами, корнем которого является a:
Раз a- корень квадратного уравнения, значит и сопряженное ему комплексное число тоже будет корнем этого уравнения и, следовательно, уравнение имеет вид:
![]() , т.е.
, т.е.
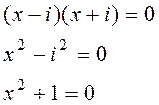
2. Задание 401-410.
Вычислить
площади фигур, ограниченных линиями а) ![]() и
и ![]() .
.
Решение. I способ
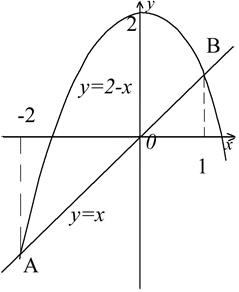
Рис.6
Найдем абсциссы точек A и B, решая совместно уравнения
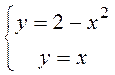 Þ
Þ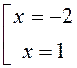
по формуле (11):
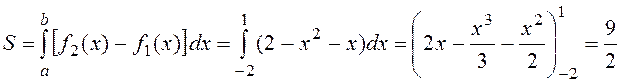
II способ:
по формуле (14):
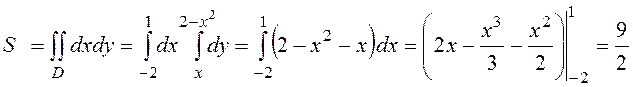
б) найти площадь одного лепестка кривой ![]() (Рис.7).
(Рис.7).

Рис.7
Решение.
I способ.
Заметим, что если полярный угол φ изменяется от 0 до π, то точка на кривой обходит против часовой стрелки один лепесток; поэтому по формуле (12) для искомой площади имеем:
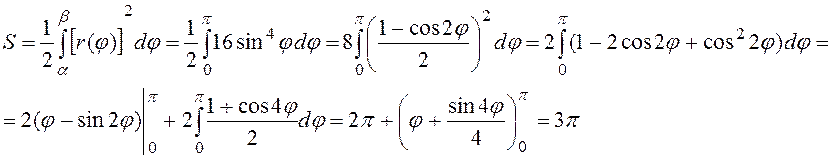 II способ.
II способ.
по формуле (17) имеем:
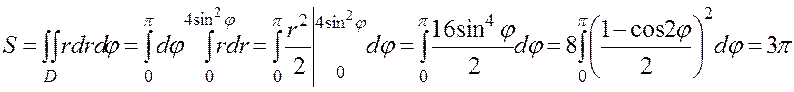
3. Задание 411-420.
Изменить
порядок интегрирования в повторном интеграле 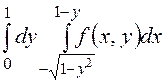 , предварительно
изобразив на чертеже области интегрирования.
, предварительно
изобразив на чертеже области интегрирования.
Решение. Строим область Dпо пределам интегрирования
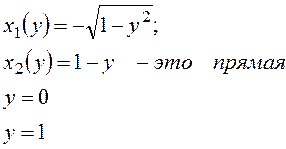
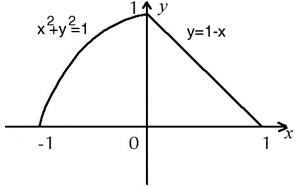
Рис.8
Область такова, что при вычислении
внешнего интеграла по переменной ![]() верхняя
граница области D описывается двумя уравнениями
верхняя
граница области D описывается двумя уравнениями
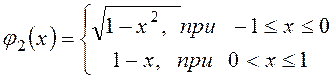 , следовательно, будем иметь
, следовательно, будем иметь
![]()
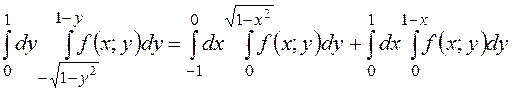 .
.
4. Задание 441-450.
Найти
работу, производимую силой ![]() , вдоль параболы
, вдоль параболы ![]() от точки А(0,0) до точки В(1,1).
от точки А(0,0) до точки В(1,1).
Решение. Из формулы (26) следует, что 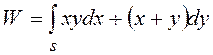 .
Так как интегрируем по параболе
.
Так как интегрируем по параболе ![]() и при перемещении из
точки А в точку В
и при перемещении из
точки А в точку В ![]() меняется от 0 до 1(Рис.9),
получаем по формуле (23), учитывая, что
меняется от 0 до 1(Рис.9),
получаем по формуле (23), учитывая, что ![]() :
:
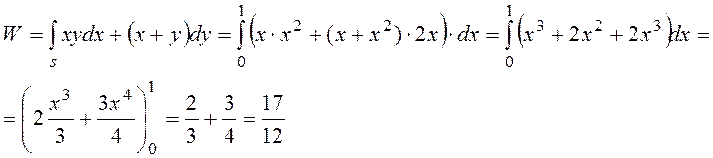
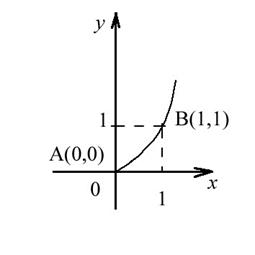
Рис.9
III. Задания к контрольной работе.
1. Задание 361-370.
Дано комплексное число a.
Требуется:
а) записать данное число в алгебраической, тригонометрической и показательной формах;
б) изобразить aна комплексной плоскости;
в) вычислить ![]()
г) найти все корни уравнения ![]() ;
;
д) вычислить произведение полученных корней;
е) составить квадратное уравнение с действительными коэффициентами
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.