Петербургский государственный университет путей сообщения
Кафедра «Высшая математика»
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Методические указания для студентов заочного факультета с примерами выполнения контрольных работ
2006
§1. Частные производные
Пусть ![]() и
и
![]() - приращения переменных
- приращения переменных ![]() и
и ![]() соответственно.
Введём обозначения
соответственно.
Введём обозначения
![]() ,
(1.2)
,
(1.2)
![]() , (1.3)
, (1.3)
![]() .
(1.4)
.
(1.4)
![]() будем называть частным приращением
функции по переменной
будем называть частным приращением
функции по переменной ![]() ,
, ![]() -
частным приращением функции по переменной
-
частным приращением функции по переменной ![]() ,
, ![]() - полным приращением функции (или просто
приращением).
- полным приращением функции (или просто
приращением).
Частной производной функции ![]() по переменной
по переменной ![]() называется предел отношения частного
приращения функции
называется предел отношения частного
приращения функции ![]() по
по ![]() к
приращению
к
приращению ![]() при стремлении
при стремлении ![]() к нулю.
к нулю.
Частную производную функции ![]() по переменной
по переменной ![]() обозначают
одним из символов
обозначают
одним из символов ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Таким образом, 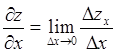 .
.
Аналогично
частную производную функции ![]() по переменной
по переменной ![]() обозначают одним из символов
обозначают одним из символов ![]() ,
, ![]() ,
, ![]() ,
,![]() и по определению
и по определению
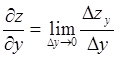 .
.
Для функции ![]() переменных
переменных ![]() частная
производная по переменной
частная
производная по переменной ![]() имеет вид
имеет вид
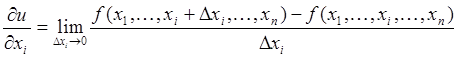 .
.
Из определения следует, что правила вычисления частных производных совпадают с правилами дифференцирования функции одной переменной, но при вычислении частных производных полагают, что другие переменные (по которым не производится дифференцирование) принимают постоянные значения.
Пример 1.1. Найти частные производные функции ![]() .
Для нахождения
.
Для нахождения ![]() полагаем
полагаем ![]()
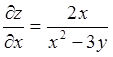 .
.
Для
нахождения ![]() полагаем
полагаем ![]()
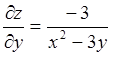 .
.
Пример
1.2. Найти частную производную по
переменной ![]() функции
функции ![]() .
Полагая
.
Полагая ![]() и
и ![]() ,
находим
,
находим 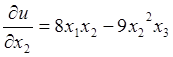 .
.
§2. Дифференциал функции нескольких переменных
Рассмотрим функцию (1.1) и её приращение
(1.4). Если функция ![]() в точке
в точке ![]() имеет
непрерывные частные производные
имеет
непрерывные частные производные ![]() и
и ![]() , то её приращение представимо в виде
, то её приращение представимо в виде
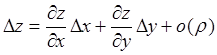 ,
(2.1)
,
(2.1)
где
![]() ;
; ![]() -
бесконечно малая более высокого порядка малости по сравнению с
-
бесконечно малая более высокого порядка малости по сравнению с ![]() .
.
Сумма
первых двух слагаемых в выражении (2.1) линейно зависит от ![]() и
и ![]() и
представляет собой главную часть приращения.
и
представляет собой главную часть приращения.
Если приращение функции ![]() представимо в виде
(2.1), то функция называется дифференцируемой в точке
представимо в виде
(2.1), то функция называется дифференцируемой в точке ![]() ,
а линейная часть приращения называется дифференциалом и обозначается через
,
а линейная часть приращения называется дифференциалом и обозначается через ![]() или
или ![]() .
.
Из определения и формулы (2.1) следует
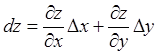 .
(2.2)
.
(2.2)
Введем обозначения ![]() и
и ![]() . Тогда
. Тогда
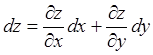 .
(2.3)
.
(2.3)
Пример
2.1. Найти дифференциал функции ![]() . Находим сначала частные производные
. Находим сначала частные производные 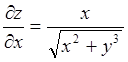 ;
; 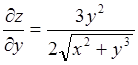 .
.
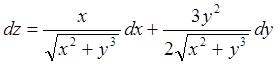 .
(2.4)
.
(2.4)
Из формулы (2.1) следует, что приращение функции ![]() и её
дифференциал
и её
дифференциал ![]() отличаются на бесконечно малую более
высокого порядка малости по сравнению с
отличаются на бесконечно малую более
высокого порядка малости по сравнению с ![]() . В
приближённых вычислениях полагают
. В
приближённых вычислениях полагают ![]() . Тогда справедливо
приближённое равенство:
. Тогда справедливо
приближённое равенство:
![]() . (2.5)
. (2.5)
Пример
2.2. Вычислить приближенно![]() , заменив приращение функции
дифференциалом. Введем функцию
, заменив приращение функции
дифференциалом. Введем функцию ![]() .
. ![]() . Используя
(2.5), получим
. Используя
(2.5), получим
![]() .
.
Дифференциал
![]() найден в примере 2.1. Для нахождения
найден в примере 2.1. Для нахождения ![]() подставим в формулу (2.4) следующие
значения:
подставим в формулу (2.4) следующие
значения:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
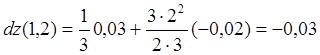 .
.
![]() .
.
§3. Уравнения касательной плоскости и нормали к поверхности
![]() (3.1)
(3.1)
в пространстве задаёт некоторую поверхность. Уравнение (1.1) является частным случаем уравнения (3.1).
Пусть ![]() - точка поверхности,
заданной уравнением (3.1). Плоскость, в которой расположены касательные прямые
к кривым на поверхности, проходящим через точку
- точка поверхности,
заданной уравнением (3.1). Плоскость, в которой расположены касательные прямые
к кривым на поверхности, проходящим через точку ![]() ,
называется касательной плоскостью к поверхности в точке
,
называется касательной плоскостью к поверхности в точке ![]() .
.
Уравнение касательной плоскости имеет вид
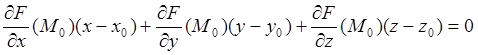 . (3.2)
. (3.2)
Прямая, проведенная через точку ![]() перпендикулярно касательной плоскости, называется
нормалью к поверхности в точке
перпендикулярно касательной плоскости, называется
нормалью к поверхности в точке ![]() . Уравнение нормали
имеет вид
. Уравнение нормали
имеет вид
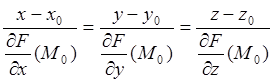 .
(3.3)
.
(3.3)
или в параметрической форме![]()
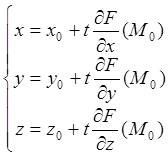 ,
,
![]() . (3.4)
. (3.4)
Пример
3.1. Найти уравнения касательной плоскости и нормали к поверхности ![]() в
точке
в
точке ![]() . Приведем уравнение поверхности к виду
(3.1)
. Приведем уравнение поверхности к виду
(3.1)
![]() .
.
![]() ;
; ![]() ;
;![]() ;
;![]() .
.
Находим частные производные.
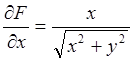 ;
; 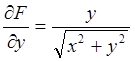 ;
;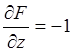 .
.
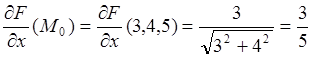 ;
; 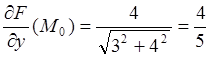 ;
;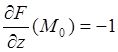 .
.
Используя (3.2), находим уравнение касательной плоскости
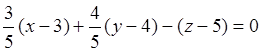
или
![]() .
.
Используя (3.3), находим уравнение нормали
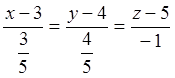
или
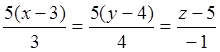 .
.
§4. Частные производные высших порядков
Рассмотрим функцию двух переменных (1.1). Её частные производные ![]() и
и ![]() также
являются функциями двух переменных и могут быть продифференцированы как по
также
являются функциями двух переменных и могут быть продифференцированы как по ![]() , так и по
, так и по ![]() . Второй
производной от функции
. Второй
производной от функции ![]() по
по ![]() ,
называется производная по
,
называется производная по ![]() от
от ![]() . То есть
. То есть![]()
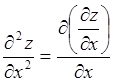 .
(4.1)
.
(4.1)
Второй
производной от функции ![]() по
по ![]() ,
называется производная по
,
называется производная по ![]() от
от ![]() . То есть
. То есть![]()
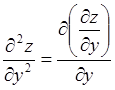 .
(4.2)
.
(4.2)
Если ![]() продифференцировать по
продифференцировать по![]() , то получим вторую смешанную производную
, то получим вторую смешанную производную
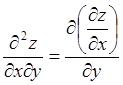 .
(4.3)
.
(4.3)
Если ![]() продифференцировать по
продифференцировать по![]() , то получим еще одну смешанную производную
второго порядка
, то получим еще одну смешанную производную
второго порядка
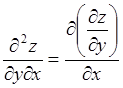 .
(4.4)
.
(4.4)
Аналогично вводятся производные третьего и более
высокого порядка. Например, 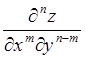 - производная
- производная ![]() -го порядка; функция
-го порядка; функция ![]() сначала
сначала ![]() раз
дифференцируется по
раз
дифференцируется по ![]() , а затем -
, а затем - ![]() раз по
раз по ![]() . Если
функция
. Если
функция ![]() имеет непрерывные частные производные, то
при нахождении смешанных производных порядок дифференцирования не играет роли.
То есть
имеет непрерывные частные производные, то
при нахождении смешанных производных порядок дифференцирования не играет роли.
То есть
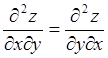 ,
,
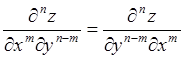 .
.
Пример
4.1. Найти частные производные
второго порядка функции ![]() . Найдем сначала
. Найдем сначала ![]() и
и ![]() .
. 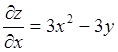 ;
; 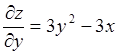 .
.
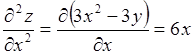 ;
; 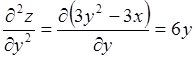 ;
;
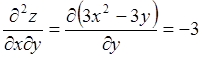 ;
; 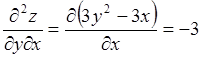 .
.
§5. Экстремумы функции двух переменных
Рассмотрим функцию ![]() , определенную в некоторой
области
, определенную в некоторой
области ![]() , содержащей точку
, содержащей точку ![]() .
.
Будем говорить, что функция ![]() имеет максимум в точке
имеет максимум в точке ![]() , если у
, если у ![]() существует
такая окрестность, что для всех точек
существует
такая окрестность, что для всех точек ![]() из этой
окрестности, справедливо неравенство
из этой
окрестности, справедливо неравенство
![]() .
.
Будем говорить, что функция ![]() имеет минимум в точке
имеет минимум в точке ![]() , если у
, если у ![]() существует
такая окрестность, что для всех точек
существует
такая окрестность, что для всех точек ![]() из этой
окрестности, справедливо неравенство
из этой
окрестности, справедливо неравенство
![]() .
.
Максимум и минимум функции называются экстремумами функции.
Теорема1(Необходимые условия экстремума).
Если
функция ![]() имеет экстремум в точке
имеет экстремум в точке ![]() и дифференцируема в этой точке, то частные
производные первого порядка в точке
и дифференцируема в этой точке, то частные
производные первого порядка в точке ![]() равны нулю, то есть
равны нулю, то есть
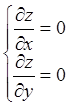 . (5.1)
. (5.1)
Точки, в которых выполняются условия (5.1) называются стационарными точками.
Функция ![]() может иметь экстремум только в
стационарных точках или в точках, в которых
может иметь экстремум только в
стационарных точках или в точках, в которых ![]() и
и ![]() не существуют. Все эти точки называют
критическими точками функции или точками возможного экстремума.
не существуют. Все эти точки называют
критическими точками функции или точками возможного экстремума.
Теорема2 (Достаточные условия экстремума).
Пусть
в некоторой окрестности стационарной точки ![]() функция
функция
![]() дважды дифференцируема, и все частные
производные второго порядка непрерывны в этой точке. Введем обозначения:
дважды дифференцируема, и все частные
производные второго порядка непрерывны в этой точке. Введем обозначения:
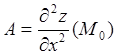 ;
; 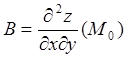 ;
; 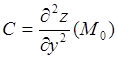 ;
; ![]() .
(5.2)
.
(5.2)
Если ![]() и
и ![]() , то
, то ![]() имеет
минимум в точке
имеет
минимум в точке ![]() ; если
; если ![]() и
и ![]() , то
, то ![]() имеет
максимум в точке
имеет
максимум в точке ![]() ;
;
если ![]() , то
, то ![]() не имеет экстремума в точке
не имеет экстремума в точке ![]() ;
;
если ![]() ,
то
,
то ![]() может иметь
и может не иметь экстремум в точке
может иметь
и может не иметь экстремум в точке ![]() , требуется
дополнительное исследование.
, требуется
дополнительное исследование.
Пример
5.1. Найти экстремумы функции ![]() . Определяем частные производные первого
порядка
. Определяем частные производные первого
порядка
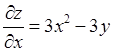 ;
; 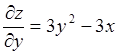 .
. ![]() и
и ![]() существуют
во всех точках плоскости. Стационарные точки находим из системы (5.1)
существуют
во всех точках плоскости. Стационарные точки находим из системы (5.1)
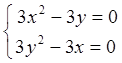 .
(5.3)
.
(5.3)
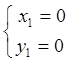 и
и 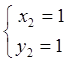 . Следовательно, функция имеет две
стационарные точки
. Следовательно, функция имеет две
стационарные точки 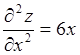 ;
; 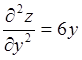 ;
;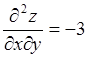 .
.
Исследуем точку![]() . Используя формулы
(5.2), находим
. Используя формулы
(5.2), находим
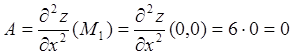 ;
; 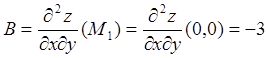 ;
;
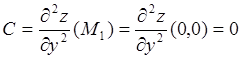 ;
; ![]() .
.
![]() .
Следовательно, в точке
.
Следовательно, в точке![]() функция не имеет экстремума.
функция не имеет экстремума.
Аналогично исследуем точку![]() .
.
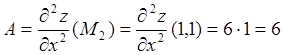 ;
; 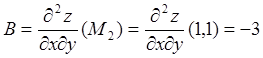 ;
;
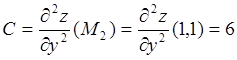 ;
; ![]() .
.
![]() и
и ![]() . Следовательно, в точке
. Следовательно, в точке![]() функция имеет минимум.
функция имеет минимум. ![]() .
.
§6. Наибольшее и наименьшее значения функции
Пусть функция ![]() непрерывна в замкнутой
ограниченной области
непрерывна в замкнутой
ограниченной области ![]() с границей
с границей![]() . Тогда она достигает в области
. Тогда она достигает в области ![]() своего наибольшего и наименьшего значений.
Если функция дифференцируема в области
своего наибольшего и наименьшего значений.
Если функция дифференцируема в области ![]() , то эти
значения достигаются либо во внутренних стационарных точках области
, то эти
значения достигаются либо во внутренних стационарных точках области ![]() либо на границе области
либо на границе области ![]() .
.
Для нахождения наибольшего и наименьшего значений следует
-
найти стационарные точки функции,
лежащие внутри области ![]() , вычислить значения
, вычислить значения ![]() в этих точках и выбрать из них наибольшее
и наименьшее.
в этих точках и выбрать из них наибольшее
и наименьшее.
-
найти наибольшее и наименьшее
значения на границе области ![]() ;
;
-
сравнить наибольшее и наименьшее
значения во внутренних стационарных точках области ![]() с
наибольшим и наименьшим значениями на границе
с
наибольшим и наименьшим значениями на границе ![]() .
.
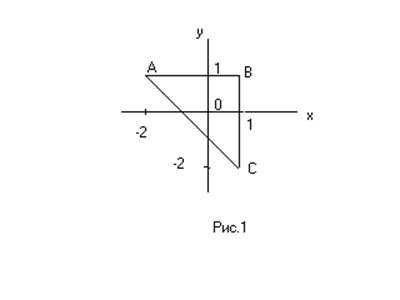 |
Область
![]() представляет собой треугольник (рис.1).
представляет собой треугольник (рис.1). 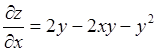 ;
; 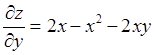 .
Система (5.1) для определения стационарных точек примет вид
.
Система (5.1) для определения стационарных точек примет вид
![]()
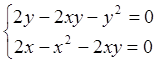 .
(6.1)
.
(6.1)
Система (6.1) имеет четыре решения
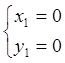 ;
; 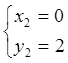 ;
; 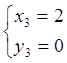 ;
; 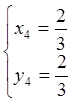 .
.
Следовательно, функция имеет четыре стационарные точки, две из которых ![]() и
и 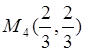 лежат внутри
области
лежат внутри
области ![]() . Вычислим значения
. Вычислим значения ![]() в
этих точках.
в
этих точках.
![]() ;
; 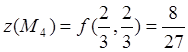 .
.
Выбирая из найденных значений наибольшее и наименьшее, получим, что внутри
области ![]()
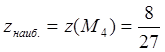 ;
;![]() .
(6.2)
.
(6.2)
Исследуем функцию на границе области ![]() . Граница
. Граница ![]() состоит из отрезков
состоит из отрезков ![]() ,
, ![]() и
и![]() .
.
Рассмотрим отрезок ![]() . Уравнение
. Уравнение ![]()
![]() ,
, ![]() .
.
Функция ![]() на границе
на границе ![]() примет вид
примет вид ![]() .
.
![]() -
функция одной переменной
-
функция одной переменной ![]() , заданная на отрезке
, заданная на отрезке ![]() , которая принимает наибольшее и наименьшее
значения либо во внутренних стационарных точках отрезка либо в его граничных
точках. Находим стационарные точки функции
, которая принимает наибольшее и наименьшее
значения либо во внутренних стационарных точках отрезка либо в его граничных
точках. Находим стационарные точки функции ![]() .
.
![]() ;
; ![]()
![]()
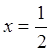 .
.
Следовательно, 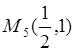 - стационарная
точка отрезка
- стационарная
точка отрезка ![]() .
.
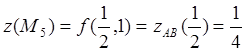 .
.
Находим значения функции в граничных точках отрезка ![]() .
.
![]() ;
; ![]() .
.
Рассмотрим
отрезок ![]() . Уравнение
. Уравнение ![]()
![]() ,
, ![]() .
.
Функция ![]() на границе
на границе ![]() примет вид
примет вид ![]() .
.
![]() -
функция одной переменной
-
функция одной переменной ![]() , заданная на отрезке
, заданная на отрезке ![]() , Находим стационарные точки функции
, Находим стационарные точки функции ![]() .
.
![]() ;
; ![]()
![]()
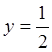 .
.
Следовательно, 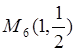 - стационарная
точка отрезка
- стационарная
точка отрезка ![]() .
.
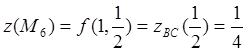 .
.
Находим значения функции в граничных точках отрезка ![]() .
. ![]() уже
найдено.
уже
найдено.
![]() .
.
Рассмотрим
отрезок ![]() . Уравнение
. Уравнение ![]()
![]() ,
, ![]() .
.
Функция![]() на границе
на границе![]() примет
вид
примет
вид ![]() .
.
![]() -
функция одной переменной
-
функция одной переменной ![]() , заданная на отрезке
, заданная на отрезке ![]() , Находим стационарные точки функции
, Находим стационарные точки функции ![]() .
.
![]() ;
; ![]()
![]()
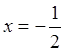 .
.
Следовательно, 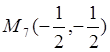 - стационарная
точка отрезка
- стационарная
точка отрезка ![]() .
.
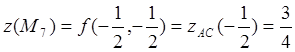 .
.
Значения
функции в граничных точках отрезка ![]() уже найдены. Выбирая
из значений
уже найдены. Выбирая
из значений ![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() , определяем наибольшее и наименьшее
значения на границе области
, определяем наибольшее и наименьшее
значения на границе области ![]() .
.
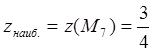 ;
; ![]() .
(6.3)
.
(6.3)
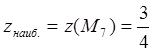 ;
; §7. Аппроксимация функций методом наименьших квадратов
Пусть некоторая функция задана таблицей значений, полученных, например, в результате эксперимента.
|
|
|
….. |
|
….. |
|
|
|
|
….. |
|
….. |
|
![]() -
значение функции в точке
-
значение функции в точке ![]()
![]() .
.
Требуется
приблизить (аппроксимировать) результаты эксперимента функцией ![]() , в которую входят параметры
, в которую входят параметры ![]() . При этом параметры подбираются таким
образом, чтобы приближенная зависимость
. При этом параметры подбираются таким
образом, чтобы приближенная зависимость ![]() была в
каком-то смысле наилучшей. В методе наименьших квадратов параметры
была в
каком-то смысле наилучшей. В методе наименьших квадратов параметры ![]() находят из условия минимума суммы
квадратов отклонений точного и приближенного значений функции в точках
находят из условия минимума суммы
квадратов отклонений точного и приближенного значений функции в точках ![]() .
.
Рассмотрим применение этого метода на примере линейной аппроксимирующей функции вида
![]() .
(7.1)
.
(7.1)
Тогда
![]() - значение функции
- значение функции ![]() в
точке
в
точке ![]() (приближенное значение);
(приближенное значение);
![]() - разность приближенного и точного
(экспериментального) значений в точке
- разность приближенного и точного
(экспериментального) значений в точке ![]() (отклонение
в точке
(отклонение
в точке ![]() );
);
![]() - квадрат отклонения в точке
- квадрат отклонения в точке ![]() .
.
Просуммировав
квадраты отклонений по всем точкам ![]() , получим сумму
квадратов отклонений
, получим сумму
квадратов отклонений
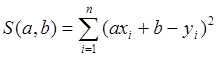 . (7.2)
. (7.2)
Найдем минимум функции ![]() как
функции двух переменных
как
функции двух переменных ![]() и
и ![]() . Вычислив частные производные
. Вычислив частные производные ![]() и
и ![]() ,
воспользовавшись необходимыми условиями экстремума (5.1) и выполнив
элементарные преобразования, получим систему уравнений
,
воспользовавшись необходимыми условиями экстремума (5.1) и выполнив
элементарные преобразования, получим систему уравнений
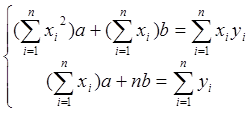 . (7.3)
. (7.3)
Система (7.3) – линейная система относительно ![]() и
и
![]() . Можно
показать, что решение этой системы (
. Можно
показать, что решение этой системы (![]() ,
,![]() ) является
точкой минимума функции
) является
точкой минимума функции ![]() .
.
Таким образом, для того чтобы найти линейную аппроксимирующую функцию достаточно
-
используя табличные значения ![]() ,
,![]() , вычислить
коэффициенты системы (7.3);
, вычислить
коэффициенты системы (7.3);
-
найти решение системы (7.3) и
подставить найденные значения ![]() и
и ![]() в функцию
(7.1).
в функцию
(7.1).
§8. Производная по направлению. Градиент
Рассмотрим функцию ![]() , определённую в области
, определённую в области ![]() , содержащей точку
, содержащей точку ![]() , и вектор
, и вектор ![]() . Из точки
. Из точки ![]() проведем луч, направление которого определяется
вектором
проведем луч, направление которого определяется
вектором ![]() , и выберем на этом луче точку
, и выберем на этом луче точку ![]() .
.
Производной функции ![]() по направлению
по направлению ![]() в точке
в точке ![]() , будем называть предел отношения
, будем называть предел отношения 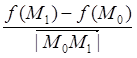 при стремлении точки
при стремлении точки ![]() к точке
к точке ![]() вдоль луча
вдоль луча ![]() . Обозначать введенную производную по
направлению будем через
. Обозначать введенную производную по
направлению будем через 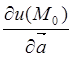 .
.
Таким образом, по определению
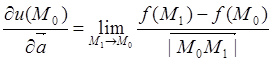 . (8.1)
. (8.1)
Если функция ![]() имеет непрерывные частные
производные первого порядка по всем переменным в области
имеет непрерывные частные
производные первого порядка по всем переменным в области ![]() , то в любой точке
, то в любой точке ![]() и
для любого направления
и
для любого направления ![]() , справедлива формула
, справедлива формула
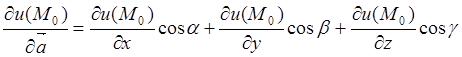 , (8.2)
, (8.2)
где
![]() ,
,![]() ,
,![]() -
направляющие косинусы вектора
-
направляющие косинусы вектора ![]() , которые вычисляются по
формулам
, которые вычисляются по
формулам
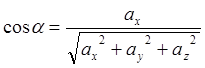 ,
,
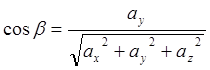 ,
, 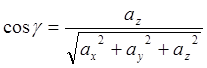 .
(8.3)
.
(8.3)
Пример 8.1. Найти производную функции ![]() по
направлению
по
направлению ![]()
![]() в точке
в точке ![]() .
.
Найдём частные производные, входящие в формулу (8.2).
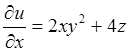 ,
, 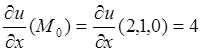 ;
;
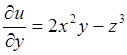 ,
, 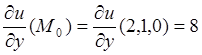 ;
;
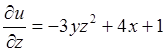 ,
, 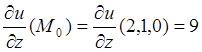 .
.
Найдём
направляющие косинусы вектора ![]() .
.
Подставляя
в (8.3) ![]() ;
; ![]() ;
; ![]() , находим
, находим
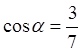 ,
,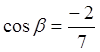 ,
,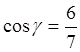 .
.
Используя (8.2), окончательно получим
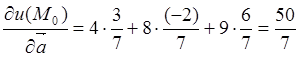 .
.
Градиентом функции ![]() в точке
в точке ![]() , будем
называть вектор
, будем
называть вектор
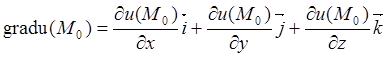 . (8.4)
. (8.4)
Пример 8.2. Найти градиент функции ![]() в
точке
в
точке ![]() . Частные
производные функции в точке
. Частные
производные функции в точке ![]() найдены в примере 8.1. Используя (8.4), получим
найдены в примере 8.1. Используя (8.4), получим ![]() .
.
Если функция ![]() зависит от двух переменных, а вектор
зависит от двух переменных, а вектор ![]() и точка
и точка ![]() принадлежат плоскости, то формулы (8.2), (8.3) и
(8.4) примут вид
принадлежат плоскости, то формулы (8.2), (8.3) и
(8.4) примут вид
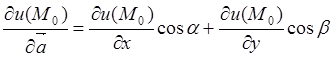 , (8.5)
, (8.5)
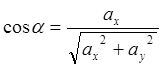 ,
, 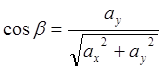 ,
(8.6)
,
(8.6)
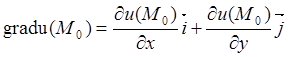 . (8.7)
. (8.7)
§9. Пример выполнения типового задания (контрольная работа 4).
Задание 1. Найти частные производные второго порядка для
функции 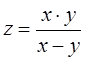 и показать, что она удовлетворяет уравнению
и показать, что она удовлетворяет уравнению
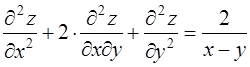 .
.
Решение:Найдём сначала частные производные
первого порядка ![]() . При вычислении частных
производных по x предполагаем, что вторая переменная yпринимает
постоянное значение. При вычислении частных производных по y
предполагаем, что вторая переменная x принимает
постоянное значение.
. При вычислении частных
производных по x предполагаем, что вторая переменная yпринимает
постоянное значение. При вычислении частных производных по y
предполагаем, что вторая переменная x принимает
постоянное значение. 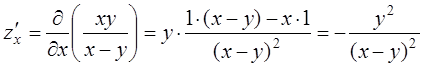 ;
; 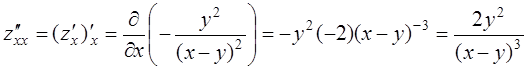 ;
; 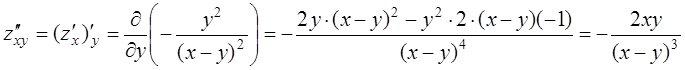 ;
; 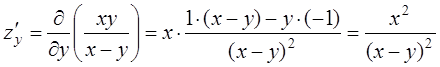 ;
; 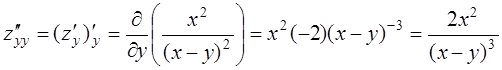 .
.
Проверим, удовлетворяет ли функция уравнению. Для этого подставим полученные
частные производные второго порядка в заданное уравнение и получим 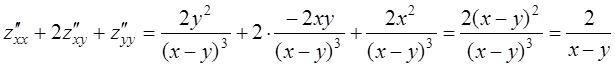 , что и требовалось доказать.
, что и требовалось доказать.
Задание 2. Дана функция ![]() и
точки А(2;1) и В(2,1;0,9).
и
точки А(2;1) и В(2,1;0,9).
Требуется:
1) вычислить точное значение функции в точке В;
2) вычислить приближённое значение функции в точке В, исходя из значения функции в точке А и заменив приращение функции при переходе от точки А к точке В дифференциалом;
3) оценить в процентах относительную погрешность;
4)
составить уравнения касательной плоскости и нормали к поверхности ![]() в точке С(2;1;z(А)).
в точке С(2;1;z(А)).
Решение: 1) Вычислим точное значение функции в точке
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.