Числовые ряды, Сходимость ряда и его сумма, Необходимое условие сходимости, Ряды с положительными членами, Признаки сравнения рядов, Признак Даламбера, Интегральный признак

Если функция f(x) имеет на некотором интервале, содержащем точку  a, производные всех порядков, то к ней может быть применена формула Тейлора

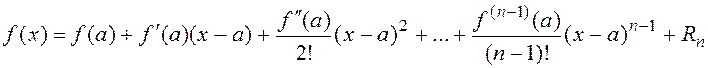, где 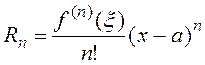    ( a< ξ < x, n – любое натуральное число).

Если для некоторого значения x  при , то в пределе формула Тейлора превращается для этого значения x в ряд Тейлора

.

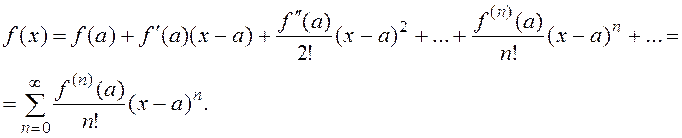В частном случае, при a=0, имеем ряд Маклорена

.

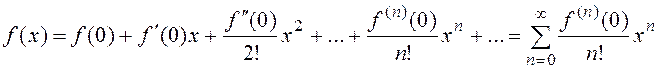Таким образом, функция f(x) может быть разложена в ряд Тейлора для рассматриваемого значения x, если:

1)  она имеет производные всех порядков;

2)  остаточный член  при  для рассматриваемого значения x.

4.3. Применение таблицы простейших разложений.

В примере 11 для определения коэффициентов разложения функции в степенной ряд пришлось прибегнуть к многократному дифференцированию, поиску значений производной в данной точке, изучению и оценке остаточного члена. Довольно часто операции последовательного дифференцирования связаны с громоздкими выкладками, а исследование стремления  к нулю доставляет еще большие трудности. Эти трудности могут быть иногда обойдены на основании теоремы единственности разложения функции в степенной ряд, позволяющей утверждать, что полученное любым путем разложение функции в степенной ряд будет ее разложением в ряд Тейлора. Для того, чтобы избежать многократного дифференцирования при разложении некоторых функций в ряды Тейлора и Маклорена могут быть использованы стандартные разложения основных элементарных функций в комбинации с правилами действия со степенными рядами.

Особенно часто при этом используют разложения по степеням x (разложения в ряд Маклорена) следующих функций:

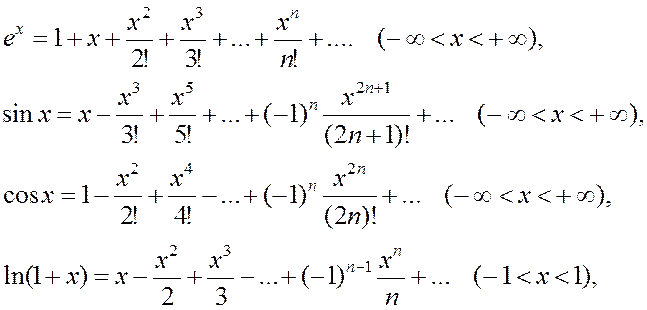
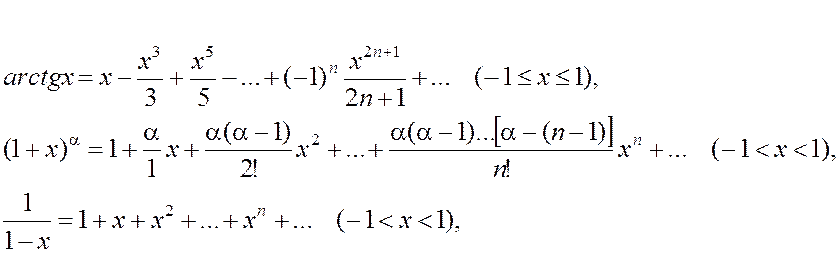
§5. Приложения степенных рядов к приближенным вычислениям

5.1. Приближенное вычисление логарифмов.

Для приближенного вычисления логарифмов удобно использовать формулу

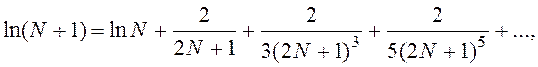
где N – натуральное число. Эта формула позволяет последовательно найти логарифмы целых чисел, причем сходимость ряда тем быстрее, чем больше N.

5.2. Приближенное вычисление корней.

Приближенное вычисление корней производится с помощью биноминального ряда

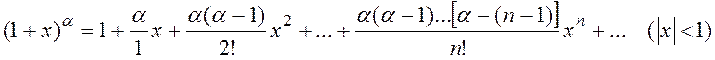
5.3. Приближенное вычисление определенных интегралов.

Многие нужные определенные интегралы не вычисляются с помощью формулы Ньютона-Лейбница, так как ее применение связано с поиском первообразной, часто не выражаемой в элементарных функциях. Однако, если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то приближенное вычисление интеграла оказывается осуществимым с наперед заданной точностью.

II. Пример выполнения контрольной работы.

1.  Задание 591-600.

Пример 1.

Исследовать на сходимость, с помощью необходимого признака, ряды:

а) 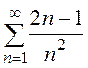  б)

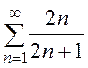
Решение.

а)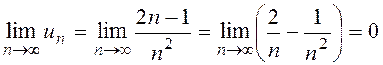

Необходимое условие сходимости ряда выполняется, но о сходимости ряда ничего нельзя сказать (как будет видно из дальнейшего, ряд расходится).

б)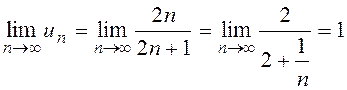

Необходимое условие сходимости ряда не выполняется и, следовательно, этот ряд расходится.

Пример 2.

Исследовать на сходимость, используя признак сравнения, ряды:

а) 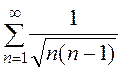  б)

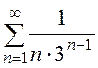
Решение.

а) Общий член данного ряда

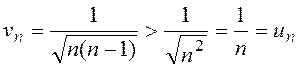, так как с увеличением знаменателя дробь уменьшается; но ряд  – гармонический, расходящийся, следовательно, данный ряд расходится и подавно.

б) Общий член данного ряда 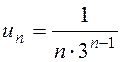   меньше общего члена сходящегося ряда геометрической прогрессии

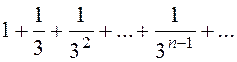, поэтому данный ряд сходится.

Пример 3.

Исследовать на сходимость, используя предельную форму признака