Закон распределения случайной величины, характеризующей надежность СЭС (P(t), f(t), l(t) и др.) - это соотношение, устанавливающее связь между значениями случайных величин и вероятностью их появления в соответствующий момент времени. Законы распределения устанавливают на основе статистических испытаний. В результате испытаний получают табличную или графическую зависимость P(t), f(t), l(t) от времени. Для упрощения дальнейшего использования результатов испытаний в теории вероятностей полученные соотношения аппроксимируют различными аналитическими зависимостями. Для наглядности в табл.1 приведены графические зависимости P(t), f(t), l(t) для экспоненциального и нормального теоретических законов распределения.
Рассмотрим характер изменения интенсивности отказов для объектов СЭС. Зависимость l от времени для объектов СЭС, построенная по результатам многочисленных наблюдений, приведена на рис.3. График l(t) может быть разбит на три отрезка по времени.
Первый отрезок t1 называется периодом приработки. За этот период происходит наибольшее число отказов, вызванных в основном скрытыми дефектами в элементах СЭС, небрежностью монтажа и т.п. Продолжительность периода приработки зависит от сложности объектов, качества монтажа и производства.
Таблица 1
Показатели, характеризующие экспоненциальный
и нормальный законы распределения
|
Закон распределения |
Экспоненциальный |
Нормальный |
|
P(t) |
P(t) t |
P(t) t |
|
f(t) |
f(t) t |
f(t) t |
|
l(t) |
l(t) t |
l(t) t |
 |
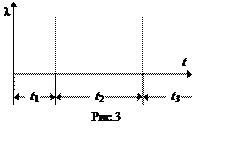Второй период t2 - период нормальной эксплуатации. В этот период число отказов уменьшается, а сами отказы носят случайный характер. Величина l(t) остается постоянной. Сравнивая функцию l(t) для второго периода с теоретическими законами распределения легко заметить, что практическое
распределение подчиняется экспоненциальному закону.
Третий период t3 - заключительный период эксплуатации, период старения вследствие износа и усталости. На данном периоде в результате необратимых физико-химических процессов число отказов увеличивается и объект (элемент) достигает своего предельного состояния.
Для основных элементов СЭС период приработки длится 3¸5 лет, период нормальной эксплуатации 15¸50 лет (для ВЛ на опорах из пропитанной древесины - 15¸20 лет, трансформаторов и кабельных ЛЭП - 20¸30 лет, коммутационной аппаратуры - 40¸50 лет). Период приработки аппаратуры З и СА 5¸120 часов.
Надежность СЭС определяется для периода нормальной эксплуатации. Поэтому при расчетах используется экспоненциальный закон распределения.
7.Поток отказов и его свойства
Т11 t11 Т12 t12 Т13
 |
Т11 t11 Т12 t12 Т13
 |
Т11 t11 Т12 t12 Т13
 |
Рис.4
Процесс функционирования элементов СЭС показан на рис.4. Элемент Т1, проработав случайное время Т11, отказывает, а затем восстанавливается за время t11. После восстановления он функционирует снова и проработав время Т12, отказывает, восстанавливается за время t12 и т.д. Совокупность отказов элементов СЭС во времени образует поток отказов.
Поток отказов называется стационарным, если вероятность появления событий на интервале tк, tк + D tк зависит от длины интервала и не зависит от момента tк начала интервала.
Поток отказов называется ординарным, если вероятность совмещения двух и более событий в один и тот же момент времени исчезающе мала, т.е.
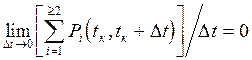, (26)
где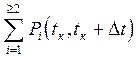 
-
вероятность отказов двух и более элементов за время от tк
до tк + Dt.
Ординарность потока отказов означает, что в момент времени tк не может быть более одного отказа.
Поток событий называется потоком без последствий, если для любых непересекающихся событий, попадающих в один из них, не зависит от числа событий, попадающих в другие интервалы. Отсутствие последствий означает, что вероятность наступления n отказов за отрезок Dt не зависит от того, сколько было отказов ранее и как они распределены во времени, то есть все отказы являются независимыми событиями.
В реальных СЭС ни одно из указанных свойств в точности не соблюдается. При отказе одного из элементов может произойти перераспределение нагрузки на оставшиеся элементы таким образом, что и эти элементы откажут, то есть нарушится отсутствие последствия. Нарушается и свойство ординарности. Однако исследования показали, что в инженерных расчетах надежности СЭС можно принять, что поток отказов удовлетворяет условиям стационарности, ординарности и отсутствия последствия. Такой поток отказов называется простейшим. При простейшем потоке отказов частота отказов
, (27)
то есть интервалы между отказами в период нормальной работы оборудования распределены по экспоненциальному закону.
В качестве параметра экспоненциального распределения восстановления используют интенсивность восстановления m. Вероятность восстановления элемента за время от 0 до t:
; (28)
среднее время восстановления:
.
Для инженерных расчетов надежности в СЭС принимается, что время безотказной работы T и время восстановления t распределяется по экспоненциальному закону.
8.Основные допущения при расчете
надежности СЭС
При расчете надежности реальная СЭС рассматривается как некоторая абстрактная структура. Отказы отдельных элементов СЭС рассматриваются как независимые события, а потоки отказов, восстановлений и технического обслуживания - как простейшие потоки событий, для которых справедливы следующие соотношения: l(t) = l = w = const и m = const. Пропускная способность элементов СЭС не ограничена.
Для реальной системы электроснабжения составляется схема замещения. Каждый элемент схемы замещения имеет вход и выход и может находится в двух состояниях: работоспособном и неработоспособном. Соединения элементов на схеме замещения соответствуют соединению представляемых ими реальных элементов на схеме СЭС. Показатели надежности элементов принимаются в соответствии с данными таблицы 2.
9. Расчет надежности структуры с последовательным соединением элементов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
