Методические указания к изучению дисциплины "Надежность систем электроснабжения", страница 2

Статистически вероятность безотказной работы определяется по формуле:

, (3)

где  N(t) - число безотказно проработавших элементов до момента времени t;

N(0) - первоначальное число наблюдаемых элементов.

Вероятность отказа статистически определяется из уравнения:

, (4)

где  n(t) - число элементов, отказавших к моменту времени t.

При N(0) ® ¥ статистические параметры P*(t) и Q*(t) стремятся к вероятностям P(t) и Q(t).

Обозначим:

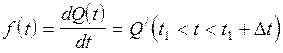. (5)

Переменная f(t) называется плотностью вероятности отказа.

Очевидно, что

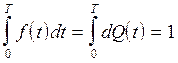. (6)

Статистически f(t) определяется как отношение числа отказавших элементов n(t, t+Dt) на интервале Dt к произведению первоначально наблюдаемого числа элементов N(0) на длительность рассматриваемого интервала времени, т.е.:

. (7)

Из уравнений (1) и (5) следует, что

. (8)

f(t)

f(t_i)

Dt_i

t_i                               t

Рис.2

Плотность вероятности отказа имеет размерность год^-1. Так как Q(t) увеличивается с ростом t, то плотность вероятности отказа всегда положительна.

Рассмотрим случай, когда величина T задана плотностью вероятности отказа f(t_i). Допустим, что все возможные значения наработок на отказ принадлежат отрезку времени 0¸t. Разобьем данный отрезок на n частичных отрезков длиной Dt₁, Dt₂,..., Dt_i,..., Dt_n (рис.2) и

выберем в каждом из них произвольную точку t_i. Составим сумму

. (9)

Произведение f(t_i)Dt_i приближенно равно вероятности того, что в течение времени Dt_i наступит отказ объекта. Переходя к пределу при Dt_i стремящемся к нулю и n ® ¥, получим определенный интеграл:

.

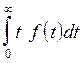Данный интеграл равен математическому ожиданию наработки на отказ:

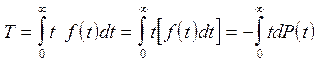. (10)

Проинтегрируем выражение (10) по частям

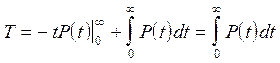. (11)

Интенсивность отказов - это взятое для одного и того же момента времени отношение плотности вероятности отказа к вероятности безопасной работы:

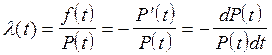. (12)

Возьмем интеграл:

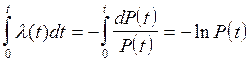. (13)

Потенциируя (13), получим, что вероятность безотказной работы P(t) равна:

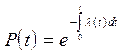. (14)

Таким образом, вероятность безотказной работы любого объекта в любой момент времени может быть вычислена по формуле (14), если известна зависимость интенсивности отказов от времени.

Статистически величина l(t) определится по формуле:

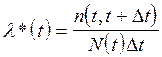 (15)

3.Показатели, характеризующие ремонтопригодность элементов СЭС

Ремонт - это совокупность мер, предпринимаемых для восстановления работоспособности объекта.

Восстановление - это событие, заключающееся в переходе объекта из неработоспособного состояния в рабочее состояние.

Вероятность восстановления элемента за заданное время - вероятность того, что время восстановления t_в элемента не превысит заданное время t_з

. (16)

Статистически G(t) определяется как отношение числа случаев m(t_в<t_з), когда восстановление элемента длилось меньше интервала t_з, к числу наблюдаемых случаев восстановления M

. (17)

Среднее время восстановления - это математическое ожидание времени восстановления

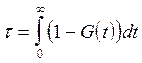. (18)

Статистически t* - суммарное время восстановления, зафиксированное за M случаев восстановления, отнесенное к количеству этих случаев

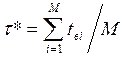. (19)

Вероятность нахождения элемента в работоспособном состоянии - это вероятность того, что в произвольный момент времени элемент находится в работоспособном состоянии. Для установившегося режима вероятность нахождения элемента в работоспособном состоянии называется коэффициентом готовности. Для всех законов распределения

. (20)

Коэффициент простоя - это вероятность того, что в установившемся режиме в произвольный момент времени элемент будет неработоспособен. Очевидно, что

. (21)

Коэффициент оперативной готовности - вероятность безотказной работы элемента в течение заданного времени работы t в период нормального функционирования при условии, что до этого момента элемент не отказал

. (22)

4.Показатели, характеризующие преднамеренные

отключения элементов СЭС

Элемент системы может быть выведен из работы не только из-за потери работоспособности, но и для выполнения каких-либо работ, как на самом элементе, так и на элементах с ним взаимосвязанных. Например, для проведения планово-предупредительных ремонтов на оборудовании, устранения дефектов, увеличивающих опасность отказа, выполнения работ вблизи элемента, находящегося под высоким напряжением. Такие отключения называются преднамеренными, поскольку они выполняются направленными действиями персонала, обслуживающего оборудование.

С целью упрощения модели функционирования элементов при оценке преднамеренных отключений используются показатели, аналогичные показателям, характеризующим отказы и восстановления, а именно: частота преднамеренных отключений n и среднее время технического обслуживания (восстановления после преднамеренного отключения) h. Статистически n и h определяются по формулам:

; (23)

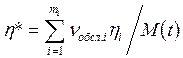, (24)

где   m^/(t,t+Dt) - число преднамеренно отключенных элементов на интервале (t,t+Dt);

M(t) - число наблюдаемых элементов;

n_обсл.i и h_i - частота преднамеренных отключений и время технического обслуживания i-го элемента;

m₁ - число наблюдаемых случаев преднамеренных отключений.

 Среднее время технического обслуживания h используют при определении коэффициента технического использования элемента.

Коэффициент технического использования элемента СЭС вычисляют по формуле

. (25)