Приведенные ниже задачи, как правило, не являются целочисленными по своей постановке, т.е. в постановке этих задач нет требования целочисленности искомых переменных. Тем не менее, результирующие модели являются либо моделями булевского программирования, либо после соответствующего преобразования мы получаем модели целочисленного или частично целочисленного линейного программирования. Используемые в этих моделях булевские или целочисленные переменные, как правило, являются искусственными, введенными в модель для целей формализации некоторых плохо формализуемых условий (например, учет постоянных издержек в целевой функции). При рассмотрении приведенных ниже задач рекомендуется обратить особое внимание на моделирование такого рода условий, а также на то, в какой степени усложняется получаемая в результате этих построений модель.
Задача 1.13. Задача с фиксированными доплатами
Рассмотрим задачу планирования производства N видов продукции при условии, что производство j-го вида продукции связано с постоянными затратами в размере Kj [7,т.1].Величина постоянных затрат Kj не зависит от объема производства этого вида продукции (например, аренда помещения, оплата персонала, не связанного непосредственно с выпуском продукции, например, бухгалтера, и др.). Кроме постоянных затрат, имеются переменные затраты на производство, пропорциональные объему выпуска продукции (заработная плата непосредственного изготовителя, расход материалов, энергии и др.). При этом стоимость единицы продукции j-го вида равна Cj. Допустим, что имеется M видов ресурсов и при производстве единицы продукции вида j расходуется aij единиц ресурса i-го вида. Кроме того, известно, что имеется возможность реализации dj единиц продукции j-го вида по цене pj долл. Запас ресурсов i-го вида ограничен величиной bj (i = 1, 2, ..., M). Требуется определить оптимальные пропорции производства продукции с целью получения максимальной чистой прибыли.
Величина общих производственных затрат, равная сумме постоянных и переменных затрат, представляет собой нелинейную функцию объема выпуска продукции. Но, если использовать булевы переменные, можно сформулировать эту задачу в виде задачи булева программирования. Затем полученную задачу с помощью стандартного преобразования можно свести к задаче ЦЛП.
Пусть булева переменная dj соответствует принятию решения о производстве j-го вида продукции. Другими словами,
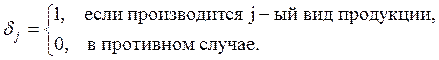
Пусть xj ≥ 0 обозначает объем выпуска j-го вида продукции. Тогда общие затраты на производство j-го вида продукции составляют Kjδj + Cjxj, где δj = 1, если xj> 0 и δj = 0 при xj = 0.
Таким образом, целевая функция имеет вид:
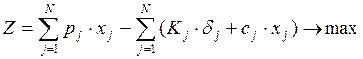 .
.
Ограничения по i-му виду ресурсов можно записать следующим образом:
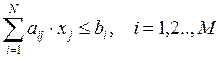 .
.
Ограничения, связанные с объемом спроса, имеют вид:
![]() ;
;
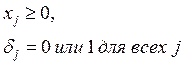
Заметим, что значение xj должно быть положительным только при δj = 1; в этом случае производство j-го вида продукции ограничено величиной dj и в целевую функцию включаются постоянные затраты Kj.
Вопросы для обсуждения:
1. С помощью какого преобразования задачу булева программирования можно свести к задаче ЦЛП?
2. Какие ограничения модели
обуславливают недопустимость решения, при котором объем продукции положителен (![]() ), а соответствующие постоянные
издержки равны нулю (т.е. переменная
), а соответствующие постоянные
издержки равны нулю (т.е. переменная ![]() )?
)?
3. Как вы поясните тезис о том, что целевая функция исходной задачи является нелинейной?
Задача 1.14. Задача о твердых отходах
Управляющие решения в области сбора и удаления твердых отходов связаны с планированием работы предприятий и использованием оборудования. Состав и количество твердых отходов, образующихся в текущем периоде, или соответствующие прогнозные оценки, обычно рассматриваются как входной поток системы, и основное внимание уделяется сбору, транспортировке, накоплению, обработке и уничтожению этих отходов [7,т.1].
Теоретически процесс принятия решений включает две стадии. На первой стадии определяется желаемый характер обслуживания, а на второй — методы реализации такого обслуживания с минимальными затратами. С точки зрения моделирования система удаления твердых отходов включает следующие элементы: источники отходов, стационарные сооружения и оборудование для перемещения, обработки и уничтожения отходов, средства транспортировки отходов и персонал системы. Большинство математических моделей таких систем являются оптимизационными, в частности, задачи выбора сооружений (предприятий) и мест их размещения, которые обычно являются моделями частично целочисленного программирования. В этом случае задача может быть сформулирована следующим образом:
Найти ![]()
при ограничениях
![]() для
каждого i-ого источника,
для
каждого i-ого источника,
![]() для
каждого j-ого пункта,
для
каждого j-ого пункта,
![]() - целые числа,
равные 0 или 1,
- целые числа,
равные 0 или 1,
где
· Yj = 1 – если сооружение строится в j-ом пункте, 0 – в противном случае;
· Fj – постоянные затраты на строительство такого сооружения;
· Dj – затраты на ликвидацию 1 т отходов на мусоросжигательной станции в j-ом пункте;
· Tij – затраты на перевозку 1 т отходов от i-го источника (зоны сора) до j-го пункта;
· ai - количество отходов, образующееся в i-ой зоне сбора;
· bj - производственная мощность в j-ом пункте;
· Xij – количество отходов, которое должно быть перевезено из i-ой зоны сбора в j-ый пункт.
Первая группа ограничений соответствует требованию, согласно которому отходы, накапливаемые в каждой из зон, должны быть собраны и вывезены полностью. Вторая группа ограничений выражает условие, согласно которому поток отходов, направленный на соответствующее сооружение, не превышает его мощности по переработке.
Вопросы для обсуждения:
1. Модель, полученная после преобразований, является полностью или частично целочисленной?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.