Примеры задач целочисленного линейного программирования. Задача оптимального размещения углеобогатительных фабрик, страница 2

2. Как учитывается в модели ограниченная мощность перерабатывающих фабрик?

Задача 1.15. Задача оптимального размещения углеобогатительных фабрик

В Соединенных Штатах Америки для каждого штата установлены строгие нормы по выбросу серы. Поэтому при решении задачи о возможности строительства централизованных фабрик по обогащению угля с произвольным содержанием серы учитывались заданные нормативы, что позволяло спланировать площадки для строительства c целью дальнейшего получения угля, удовлетворяющего одновременно нуждам потребителей и стандартам по охране окружающей среды [7 ,т.1].

С помощью механического процесса на централизованных обогатительных фабриках уголь перерабатывается в смесь, которая должна удовлетворять природоохранным нормам. Требовалось ответить на следующие вопросы:

·  Сколько нужно построить углеобогатительных фабрик?

·  Где их нужно строить?

·  Каких потребителей должна обслуживать фабрика и где добывать уголь?

·  Каковы оптимальные соотношения различных углей, предназначенных для переработки, которые удовлетворяют нормам по охране окружающей среды?

Для получения ответов на эти вопросы была разработана однопериодная (статическая) модель.

Переменные модели. Индексы i, j, k используются для обозначения индексов (номеров) шахт, обогатительных фабрик и потребителей.

·  v_ij – вес угля (в тоннах), отправленного из шахты i на обогатительную фабрику в районе j.

·  u_jk – вес угля, отправленного с обогатительной фабрики в районе j потребителю k.

·  w_ij – булева переменная; полагаем w_ij = 1, если уголь отправляется из шахты i в район j, в противном случае wij = 0.

·  x_jk – булева переменная; полагаем x_jk = 1, если уголь отправляется из района j потребителю k, в противном случае x_jk = 0.

·  y_j – булева переменная; y_j = 1, если для строительства фабрики используется район j, в противном случае y_j =0.

Целевая функция. Требуется минимизировать все затраты системы, в том числе следующие:

·  стоимость различных видов угля (в $ за тонну) при шахтной добыче.

·  стоимость переработки, куда входят капитальные затраты на строительство обогатительной фабрики и переменные затраты, пропорциональные объему перерабатываемого угля.

·  транспортные затраты, которые зависят от места добычи, назначения и количества груза. Транспортные издержки включают постоянные издержки, не зависящие от количества перевозимого угля, и переменную часть, пропорциональную расстоянию и объему перевозимого угля.

Таким образом ,целевая функция системы имеет вид

,

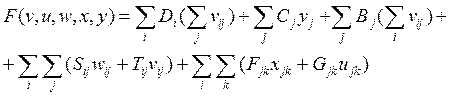где

·  D_i – стоимость добычи на шахте i тонны угля;

·  S_ij – постоянные расходы на перевозку угля из шахты i на обогатительную фабрику в районе j;

·  T_ij – стоимость перевозки тонны угля из шахты i на фабрику в районе j;

·  С_j – ежегодные постоянные затраты на переработку тонны угля на фабрике в районе j;

·  B_j – переменные затраты на переработку тонны угля на фабрике в районе j;

·  F_jk –постоянные расходы на перевозку с фабрики в районе j потребителю k;

·  G_jk – стоимость перевозки тонны угля с фабрики в районе j потребителю k.

Ограничения системы. Моделируемую систему описывают следующие ограничения.

Вес перевозимого угля не может превысить мощности шахты по добыче угля:  для всех i, где M_i – мощность шахты i по добыче угля.

Объем поставок потребителю должен удовлетворять его потребности:  для всех k.

Следует отметить, что в этой модели предусмотрено, что все потребности в угле удовлетворяются.

Объем перевозки с фабрики не может превысить мощности этой фабрики:  для всех j, где P_j – мощность фабрики j и y_j = 1, если фабрика работает.

Общий объем перевозок обогащенного угля с фабрики не больше (с поправочный коэффициентом) объема угля, доставляемого с шахт на эту фабрику: для всех j, где E – показатель эффективности процесса переработки.

Желательно, чтобы ограничения гарантировали удовлетворение специальных требований потребителей по содержанию по содержанию серы в обогащенном угле. В этом исследовании предполагается, что выпускаемая смесь углей, прошедших переработку, описывается линейной комбинацией объемов различных углей. Это предположение может быть принято, поскольку эмпирический данные не опровергают, хотя и не подтверждают его. Если H_i – содержание серы (в весовых процентах) в угле из шахты i, то  – количество серы в обогащенном угле на фабрике в районе j. Если фабрика в районе j обеспечивает потребителя k (т.е. если x_jk = 1), то вводится ограничение

,

где L_k – максимально допустимая для потребителя k норма содержания серы в угле. Это дополнительное ограничение можно представить в виде

 для всех j и k,

где M – большое положительное число. Такое ограничение обуславливает получение решения, при котором фабрики производят смесь углей, удовлетворяющую требованиям потребителей, которых она обслуживает. Не трудно видеть, что если x_jk = 1, то неравенство сводится к виду , т.е. количество серы в обогащенном на фабрике в районе j угле не превысит требуемую потребителем k норму содержания серы в угле. С другой стороны, если потребитель k ничего не получает с фабрики j ( x_jk = 0), то ограничение становится избыточным.

Прочие ограничения

а) Приводимые ниже ограничения позволяют учесть в модели постоянные издержки:

 для всех j и k,

 для всех i и j, где M – большое положительное число.

б) w_ij, x_jk, y_j – булевы переменные.

в) v_ij, u_jk – неотрицательные переменные.

Вопросы для обсуждения:

1. Можно ли считать результирующую модель задачей частично целочисленного программирования?

2. Как в модели учитываются постоянные и переменные издержки?

3. В каких ситуациях в задаче возникают избыточные ограничения?