МП– это математическая дисциплина, посвященная теории и методам решения задач нахождения наибольшего или наименьшего значений скалярной функции на конечном векторном пространстве.
Задачи МП – задачи
нахождения вектора Х=(х1, х2,… хj,…, хn) такого, что целевая функция
векторного аргумента Z(Х) достигает своего max (min) значения на множестве D, заданном
ограничениями gi(Х) R bi
, i=1,2,…m, bi
– константы, R
{<,>,≤,≥,=}.
Особенности МП:
1.
X n-мерному
векторному пространству
2. Одна целевая функция и один критерий оптимальности
3. Ограничения заданы жестко с помощью функциональных зависимостей (линейных или нелинейных)
Основные этапы решения задач МП:
1. Формулировка проблемы и постановка задачи. Первоначально задачу формулируют с точки зрения заказчика, затем она постоянно уточняется исследователями.
2. Сбор данных.
3. Построение математической (оптимизационной) модели. Этот процесс называется формализацией задачи. В итоге получается модель задачи МП.
4. Определение класса модели (может быть возврат на 2 этап). В зависимости от структуры ц.ф. и ограничений, вида переменных определяют класс задачи МП (ЛП, ДинП, НЛП и т.д.). Если целевая функция Z(Х) и функции, входящие в систему ограничений gi(Х) являются линейными относительно Х, то такой раздел МП наз ЛП, иначе если хотя бы одна из функций нелинейна, то такой раздел МП называется НЛП. Если процесс принятия решения имеет многошаговый характер и возможные изменения состояния системы можно представить в виде графовой модели, то такие задачи решаются методом динамического программирования (ДП). Если на переменные наложено условие дискретности, например целочисленности, то это задача дискретного программирования. Наиболее развитый и законченный класс задач – это ЛП.
5. Определение метода решения и программного обеспечения. Каждый класс задач имеет свои методы решения и можно выбрать готовые программные продукты.
6. Получение решения.
7. Проверка (в том числе анализ на устойчивость).
8. Реализация найденного решения на практике.
На практике часто возникают задачи оптимизации решений, кот. наз. задачами ЛП, для которых характерны следующие черты:
- показатель эффективности z представляет собой линейную функцию от элементов решения x1, x2, …;
- ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.
Постановка задачи ЛП.
Необходимо найти вектор Х=(х1, х2,
…, хn)
En такой, что функция линейного вида f(x)=C1x1+ C2x2+ C3x3+ … + Cnxn→max(min) и удовлетворяющий систему линейных
неравенств:
(*)
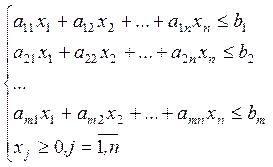или
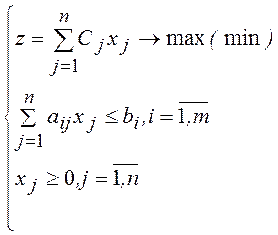
Матричная запись:
z=CX→max(min)
AX<=B
X>=0
Где C, X, B – вектор- столбцы, А-матрица mxn.
, 
, 
,
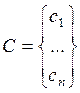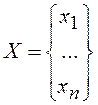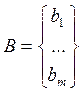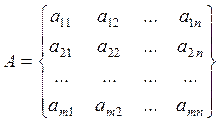
3. Взаимно-двойственные задачи ЛП
Каждой задаче ЛП (1) можно поставить в соответствие задачу, называемую двойственной (2).
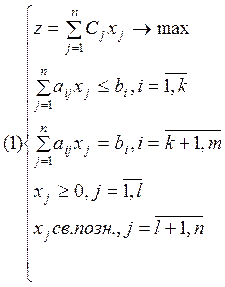
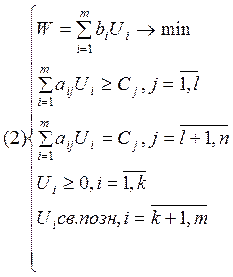
Если построить двойственную задачу по отношению к задаче (2), то получим задачу (1). Задачи 1 и 2 – взаимно-двойственные задачи ЛП.
Схема построения двойственных задач.
1. Упорядочивается запись исходной задачи, ц.ф. должна стремиться к max, ограничения-неравенства приводятся к виду ≤.
2. Число переменных двойственной задачи (2) Ui равно числу ограничений прямой задачи (1) (т.е. числу m). И наоборот, число ограничений двойственной задачи равно числу переменных прямой задачи n.
3. Свободные члены двойственной задачи (2) есть коэффициенты целевой функции задачи (1) и наоборот.
4. Максимум целевой функции в задаче (1) заменяется на минимум в задаче (2).
5. Матрица коэффициентов ограничений задачи (2) получается путем транспонирования соответствующей матрицы задачи (1).
6. Каждой переменной Ui задачи (2) соответствует i-е ограничение прямой задачи (1). И наоборот, каждой переменной прямой задачи (1) xj соответствует j-е ограничение двойственной задачи (2).
7. Если на j-ю переменную наложено условие не отрицательности, то j-е ограничение будет неравенством типа ≥, в противном случае j-е ограничение будет равенством =. Аналогично связаны между собой ограничения прямой задачи (1) и переменные задачи (2).
Пример.
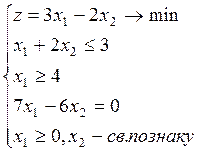приводим
к виду (1)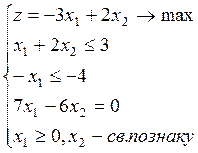 
Двойственная задача
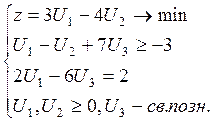
1. Если задачи (1) и (2) имеют допустимые решения, если задача (1) имеет оптимальное решение Х* , то задача (2) также имеет оптимальное решение U*. Причем значения целевых функций в оптимальных решениях равны между собой.
Z(Х*)=W(U*)
2. Если задача (1) не имеет решений вследствие неограниченности целевой функции на множестве допустимых значений, то двойственная ей задача (2) также не имеет решений вследствие противоречивости условий. Если задача (1) не имеет решений вследствие противоречивости условий, то двойственная ей задача (2) также не имеет решений вследствие неограниченности целевой функции на множестве допустимых значений.
Применение двойственных задач:
1. В вычислительных схемах алгоритмов (метод разрешимых множителей Канторовича, метод потенциалов для транспортной задачи, и др.)
2. Для проверки устойчивости полученных решений прямой задачи
3. Для качественного анализа полученного решения. Можно оценить возможность взаимозаменяемости ресурсов, если существует такая технологическая возможность.
Рассмотрим прямую и двойственную задачи в виде (3) и (4).
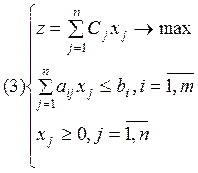
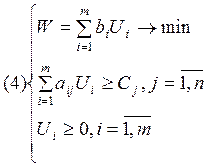
В (3) n видов производимой продукции хj, m видов ресурсов bi.
aij – постоянные коэффициенты затрат, т.е. количество ресурсов i-го вида, затрачиваемое на производство продукции j-го вида
Cj – прибыль или цена на единицу продукции j-го вида
Тогда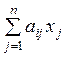 
определяет суммарное
количество i-го ресурса, необходимое для производства
набора продукции Х.
Z- прибыль или доход от производства набора продукции Х.
Приведем интерпретацию двойственной задачи (4). Из положений теории двойственности Z(Х*)=W(U*), а значит Z и W имеют одинаковые единицы измерения – денежные ед. Т.к. bi – это количество ресурса, то значит Ui – в некотором роде цена на ресурс. Поэтому двойственные переменные часто называют условными оценками.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
