Постановка задачи математического программирования (МП). Взаимно-двойственные задачи, страница 2

Рассмотрим ограничения 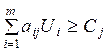.  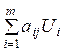 - суммарная оценка ресурсов, необходимых для производства единицы  продукции j-го вида. 

В двойственной задаче необходимо определить цены на ресурсы, так, чтобы при заданных объемах ресурса и дохода от производства продукции  минимизировать общую сумму стоимостных затрат на ресурсы.

Отсюда можно получить интерпретацию двойственности в рассматриваемой модели. Условные оценки определяют наименьшую стоимость набора ресурсов b. Ограничения двойственной задачи выражают тот факт, что если оценка затрат, необходимых для производства ед. продукции меньше цены.

Пример. Небольшая механическая мастерская с двумя типами машин выпускает изделия А и В. Изготовление единицы изделия А требует работы на машине 1 в течении 3 часов, на машине 2 – 2 часов. Изделие В изготовляется на машине 1 – 2 часа, на машине 2 – 3 часа. Машина 1 может использоваться только 8 часов в день, а машина 2 – 7 часов в день. Доход от продажи одного изделия А и В по 20. Продажа не ограничена. Определить план производства максимизирующий общий доход.

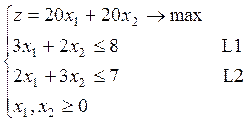, двойственная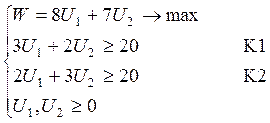

x1	0	8/3	0	3,5	U1	0	20/3	0	10
x2	4	0	7/3	0	U2	10	0	20/3	0
	L1		L2			K1		K2

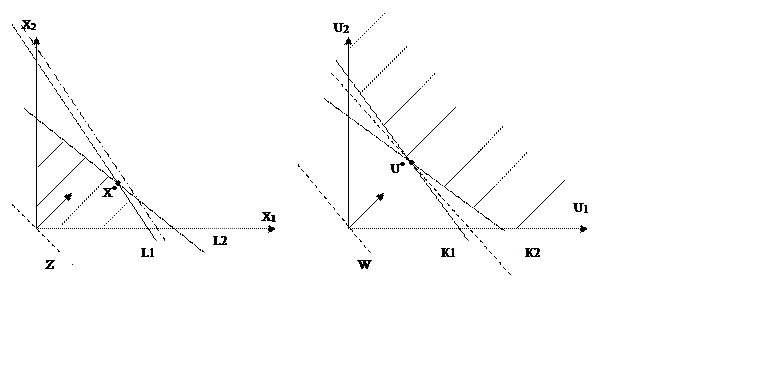
X^*(2,1), z^*=60                                      U^*(4,4), W^*=60

Т.к. U₁^*=4 дополнительная единица рабочего времени на машине 1 принесет 4 дополнительных единицы дохода (первое ограничение представляло производственные мощности первой машины).

Т.к. U₂^*=4 дополнительная единица рабочего времени на машине 2 также принесет 4 дополнительных единицы дохода (первое ограничение представляло производственные мощности первой машины).

Проверим это. Если машина 1 может работать не 8 а 9 часов, то оптимальным решением будет точка (13/5,3/5), которой соответствует доход 64, т.е. на 4 единицы больше.

x1	0	3
x2	4,5	0
L11    3x1+2x2<=9

Если руководство мастерской может арендовать 1 час работы на первом станке за 5$, а на втором станке за 3$, то следует отбросить первый вариант и воспользоваться вторым.

Закончим интерпретацию двойственных переменных. i-ая двойственная переменная (в оптимальной точке) является приращение целевой функции при ослаблении i-го ограничения на единицу.

6. Методы ЛП

Решение задач ЛП графическим методом возможно при числе переменных =2, и затруднительно уже при 3 переменных. Для нахождения решения ЗЛП в общем случае (при произвольном числе переменных) применяются вычислительные методы. Наиболее универсальный – симплекс-метод

1. Симплекс-метод (Данциг 1947 г.). Недостаток симплекс-метода – накопление ошибки в результате многоразового применения исключений Джордана-Гаусса.

Свойства симплекс-метода:

а) монотонность и конечность. Симплекс-метод является монотонным алгоритмом в том смысле, что значение целевой функции от итерации к итерации не уменьшается.

б) Алгоритм симплекс-метода – это точный метод, который сходится за конечное число шагов. Это утверждение доказывается исходя из трех положений: теоремы о существовании оптимального решения в крайней точке D, число крайних точек D конечно, перебор направленный, поэтому он конечен.

в) в случае вырождения – возможность зацикливания. В реальных расчетах такая ситуация встречается часто, а значит существует возможность зацикливания алгоритма. Существуют алгоритмы, предотвращающие эту возможность (задачник Зайченко, Шумилова).

г)  сложность метода по Реклейтису m≤k≤3m, по Моудеру 1,5m≤k≤2m, k-количество итераций. Считается, сто с.м. обладает экспоненциальной сложностью, что хуже алгоритмов с полиномиальной сложностью.

2. Двойственный симплекс-метод

3. Модифицированный симплекс-метод (метод обратной матрицы Канторовича). Дает хорошие результаты, если m<n и не велика плотность матрицы. Плотность матрицы- отношение числа ненулевых элементов к числу всех элементов матрицы.

4. Метод эллипсоидов (полиномиальный алгоритм Хачияна).

5. Алгоритм Крамаркара (1984).

7. Элементы ЦЛП

Задача ЦЛП была сформулирована Эгервари 1931 г. В 1955 первое решение задачи ЦЛП. Примеры задач ЦЛП: задача о раскрое, задача о коммивояжере.

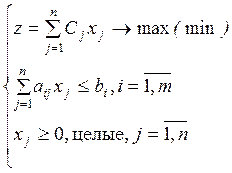
Любую задачу оптимизации можно рассматривать, как состоящей из содержания (постановка задачи) и формы (модель). Любое одно содержание можно изобразить несколькими формами. Преобразование задачи оптимизации это такое преобразование элементов модели (целевой функции и ограничений), при котором остается неизменным содержание задачи.

Например, переход от бинарной задачи к ЦЛП.

x_j={0,1} -> x_j≥0, x_j≤1, x_j –целые

Особенности множества допустимых решений D задачи ЦЛП.

1. Несвязанное множество.

2. Невыпуклое множество.

Методы решения задачи ЦЛП

1. Примитивные методы: метод простого перебора, метод приближенного решения полученного методами ЛП.

X^*»целое от( X^*_ЛП)

2. Для некоторых классов задач ЦЛП решение задачи без учета условия целочисленности является целочисленным решением. Это те задачи, для которых базисные решения (крайние точки) имеют целочисленные координаты. В частности – задача о назначении.

3. Методы ЦЛП

Точные	Приближенные
Метод отсечения. Вводится отсечение (ограничение), которое не включает полученное ранее решение и не исключает остальные.	Модификация точных методов (например, метод Гомори)
Метод ветвей и границ. Основан на эффективном способе перебора и исключении неэффективных подмножеств.	Локальной оптимизации (метод Сергиенко)
Метод последовательного анализа планов (Михайлевич)	Метод случайного поиска
Графический метод

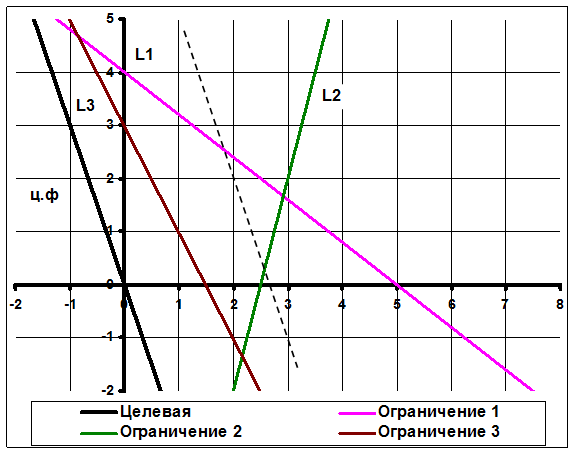
Пример на графический метод.

z = 3x₁ +x₂® max

4x₁ +5x₂  £ 20 L1

4x₁  - x₂  £ 10              L2

2x₁  + x₂  ³ 3               L3

x₁ , x₂  ³ 0

x₁ , x₂ - целые

Ответ: Х^* =(2,2), z(X*)=8