Приведенные в этом разделе задачи содержат условия, которые представляются нелинейными зависимостями. При построении соответствующих моделей иногда удается избежать включения в модель нелинейных функций и в результате получать модель линейного программирования. Иногда результирующая модель все-таки нелинейна – из класса моделей нелинейного программирования, но вследствие единичности нелинейных условий удается свести решение полученной задачи к необходимости решения последовательности задач линейного программирования. В некоторых задач полученная модель является существенно нелинейной, ее рассматривают как задачу нелинейного программирования с использованием методов решения нелинейного программирования.
При рассмотрении приведенных в этом разделе задач рекомендуется обратить внимание, как учитываются нелинейные условия исходной задачи при построении модели, при возможном ее преобразовании или на стадии решения.
Задача 1.16. Задача о смешивании
Для получения конечного продукта при перегонке нефти и приготовлении угольных смесей часто возникает необходимость смешивания нескольких видов сырья на промежуточных стадиях процесса. Это бывает обычно обусловлено ограниченностью емкостей для хранения компонентов, а также необходимостью совместной транспортировки исходных продуктов [7,т.1]. На рисунке 1.3 представлена упрощенная схема процесса смешивания двух фракций.
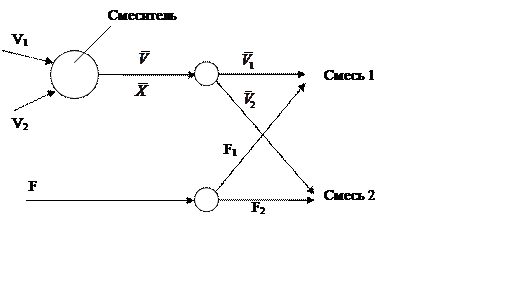
Рис. 1.3.- Схема процесса смешивания
В этой системе сначала смешивается два потока сырья: V1 c содержанием серы 3 % и V2 с содержанием серы 1 %. Полученная смесь смешивается в двух различных пропорциях с третьим потоком сырья F, имеющим 2 % серы; при этом получается 2 вида конечной смеси.
Первая смесь должна производиться в количестве не более 100 баррелей в час, причем содержание серы не должно превосходить 2,5 %; для второй смеси аналогичные показатели равны 200 баррелям в час и 1,5 %. Стоимость сырья для потоков 1, 2, 3 – равна 6, 16 и 10 долл. за 1 баррель соответственно. Продажная цена смесей составляет 9 и 10 долл. за 1 баррель соответственно. Требуется определить размеры потоков, максимизирующие доход.
Пусть Pi – выход смеси i-го вида (в баррелях в час);
· Fi – величина потока сырья третьего вида, используемого в смеси i-го вида;
· Vi – величина потока промежуточной смеси, используемой в i-ой смеси;
·
![]() –
содержание серы в промежуточной смеси.
–
содержание серы в промежуточной смеси.
Условие баланса для потоков:
![]() ,
,
![]() ,
,
![]() .
.
Условие баланса по содержанию серы:
![]() ,
,
![]() ,
,
![]() .
.
Кроме того, имеются ограничения на выход смеси:
![]() ,
, ![]()
Содержание серы в промежуточной смеси определяется содержанием серы в ее компонентах, поэтому:
![]()
Целевая функция в данном случае линейная:
![]() .
.
Задача оптимизации имеет вид:
максимизировать
![]()
при ограничениях
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
и ![]() ,
, ![]() ,
,![]()
Единственными нелинейностями задачи являются члены
вида ![]() и
и ![]() в h2, g1 и g2; в
остальном она линейна.
в h2, g1 и g2; в
остальном она линейна.
Поэтому самым простым решением здесь является
линеаризация модели с дальнейшим использованием метода линейного
программирования. С этой целью задается некоторое значение ![]() из заданного диапазона, в результате
задача становится линейной. Полученное решение задачи ЛП можно использовать для
корректировки значения
из заданного диапазона, в результате
задача становится линейной. Полученное решение задачи ЛП можно использовать для
корректировки значения ![]() ; процесс решения
задачи следует продолжать до получения удовлетворительного приближения.
; процесс решения
задачи следует продолжать до получения удовлетворительного приближения.
Вопросы для обсуждения:
1. Какие ограничения в модели являются балансовыми? Ограничения какого типа (равенства, неравенства) используются для моделирования балансовых соотношений? Почему?
2. В модели, изложенной в учебнике [7], представлены не все балансовые соотношения. Постройте недостающее ограничение.
3. Решите задачу в пакете Excel. Прокомментируйте полученный ответ.
Задача 1.17. Планирование работы гидроэнергетического комплекса
На рисунке 1.4 представлен гидроэнергетический комплекс, состоящий из двух водохранилищ и двух гидроэлектростанций, каждая из которых использует свое водохранилище [7]. Горизонт планирования работы комплекса разбит на два периода. При наполнении одного из водохранилищ избыток поступающей воды удаляется через водосброс, который также можно использовать для сброса воды в целях защиты от наводнений. Вода, проходящая через водосброс, не влияет на производство электроэнергии.
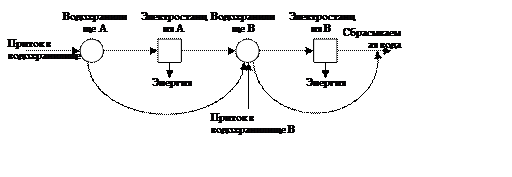
Рисунок 1.4 - Гидроэнергосистема из двух водохранилищ и двух электростанций
.
Предполагается, что один килоакр-фут (КАФ) воды на электростанции A преобразуется в 400 МВт·ч электроэнергии. Для станции B аналогичный показатель равен 200 МВт·ч. В течение одного периода станция A может произвести 60 000 МВт·ч электроэнергии, станция B – 35 000 МВт·ч электроэнергии. Цена 1 МВт·ч электроэнергии равна 20 долл. при условии, что общий объем ее реализации не превосходит 50 000 МВт·ч
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.