




 |
удк 51 (07)
У797
В установочных лекциях, состоящих из восьми частей, приводится основной теоретический материал и решение типовых задач контрольных работ по высшей математике, предлагаемых студентам-заочникам экономических и пищевых специальностей на и П курсах. Не заменяя подробных изложений курса высшей математики, изучение которых необходимо для подготовки к сдаче экзаменов, пособия позволяют выполнить контрольные работы. Правила оформления контрольных работ описаны в первой
Составители:
![]() И.Я. Глазычев,
А.М. Ивлева, А.П. Ковалевский, Л.В. Ковалевская,
И.Я. Глазычев,
А.М. Ивлева, А.П. Ковалевский, Л.В. Ковалевская,
ЕВ. Овчинникова, А.Г. Пинус, К.Н. Пономарев, СВ. Судоплатов,
ИД Черных, А.В. ЧехонаДских, ВТ. Шихова
Рецензент д-р физ.-мат. наук, проф.
Работа подготовлена на кафедре алгебры и математической логики
. ИСПЫТАНИЕ, СОБЫТИЕ. ВЕРОЯТНОСТЬ
![]() При решении мномх практических задач
При решении мномх практических задач ![]() необходимость каким10 образом оценить
возможность того или ино:о исхода в некоторой конкретной ситуации. Такие задачи
возникают, например, в страховом деле, в теории ошибок, при обрабогкс
наблюдений, в теории стрельб и др. Математическая наука, изучающая общие
закономерносм случайных явј1ений Йезависимо от их конкретной природы и даюшая
методы количественной оценки влияния случайных факторов на различные явления,
называегся теориеи вероятностей.
необходимость каким10 образом оценить
возможность того или ино:о исхода в некоторой конкретной ситуации. Такие задачи
возникают, например, в страховом деле, в теории ошибок, при обрабогкс
наблюдений, в теории стрельб и др. Математическая наука, изучающая общие
закономерносм случайных явј1ений Йезависимо от их конкретной природы и даюшая
методы количественной оценки влияния случайных факторов на различные явления,
называегся теориеи вероятностей. ![]()
В жизни мы постоянно сталкиваемся с различными испытаниями, чревапами
разнообразными исходами. Например, студент, пришедший на экзамен по высшей
математике (испытание), может получить одну из четырех опенок — ![]() 3, 4 или 5 (исходы).
3, 4 или 5 (исходы).
Как правило, при повторении испытаний частота появления разных исхолов является устойчивой величиной, т.е. имеет предел при стремлении числа испытаний к бесконечности.
Но настала пора точно определить эти ключевые понятия, которые мы широко будем использовать в дальнейшем.
Испытанием мы будет называть некоторый процесс, опыт или эксперимент, в результате которого возможно появление некоторых предсказуемых явлсний или исходов. Мы будем рассматривать только такие испытания. когорые допускаюг возможность повторения их в неизменных условиях неограниченное чисјю раз, хотя бы умозрительно. Примерами испытания может служить бросок монетки. если за возможные исходы принять выпадение «орла» и «решки», или измерение веса наугад выбранного студента университета, при этом возможпыми исходами можно считать, например, попадание и непопадание веса в заданный интервал. Конечно, число исходов в испытании может быть любым. Когда определяется испытание, необходимо указать, какие именно возможные исходы будут рассматриваться. Таким образом, вообще говоря, можно рассматривать испытание как набор возможных исходов. Событием называется появление некоторого исхода в данном испытании. Например, событие может иметь такой вид: «при броске симметричной монетки выпал «орел». Испытание в данном случае заключается в самом броске монетки, а возможных исходов всего два — выпадение «орла» и выпадение «решки». Конечно, можно предположить, что монетка упадет ребром или вообще зависнет в воздухе, но практика показывает, что такие «исходы» встречаются настолько редко, что можно их пе учитывать.
![]() Обозначать собьггия мы будет заглавными латинскими буквами.
Обозначать собьггия мы будет заглавными латинскими буквами.
Алгебра событий.
Как
и.звсспто, в большинстве своем математики ленивые люди. Для тот, кггобы
произносить поменьше слов. они готовы на всё, даже не ленятся (как это ни
парадоксально) сочинять новыс слова или придавать старым и хорошо знак'омым
совершенно новые и непонятные на первый ВЗГЛЯд смыслы. Так, например, когда они
имеюг дело с множес:гвом (т.е. набором каких-то объектов), на котором
определены какие-нибудь операции (т.е. правила, позволяющие с помощью однИХ
объектов конструировать новые, принадлежащие все тому же множеству), они
называют все это алгебраической сисаемой или (иногда) алгеброй. Поскольку
множество событий мы уже как-то определили, осзалось задать операпии.![]()
Будем рассмхгривать следующие операции над событиями. Пусть Л и В — некоторые события .
•
![]() Событием,
противоположньш А, называется событие А , означающее, что событие А не
произошло. Заметим, что при любом испытании обязательно
Событием,
противоположньш А, называется событие А , означающее, что событие А не
произошло. Заметим, что при любом испытании обязательно ![]() произойдег ровно одно из двух
взаимно противоположных событий А и А ;
произойдег ровно одно из двух
взаимно противоположных событий А и А ;![]()
• Суммой собйтий А и В называется событие А+В (или ЛИВ), означающее, стго произошло ХОтя бы одно из событий А и В;
• ПроизвеДениел событий А и В называется событие ЛВ (или АСТ), означающее, что произошли оба события А и В;
• Разностью событий А и В называется событие (или А\В), означаю[Цее, что событие А произошло, в то время как событие В не произошло.
Операции
над событиями очень напоминают операции над множествами, и это не спроста,
поскольку в сутщюсти события можно расценивать как некие наборы исходов. Суть
самих операций удобно демонстрировать на так называемых 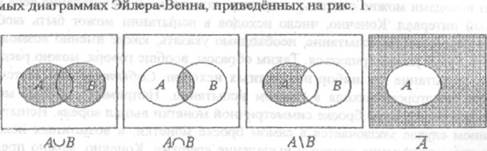 диаграммах Эйлера-Венна, приведенных
на рис. .
диаграммах Эйлера-Венна, приведенных
на рис. .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.