Установочные лекции по высшей математике. Контрольная работа. Испытание, событие, вероятность, страница 3

Определение. Сочетанием из п элементов по т элементов называется набор из т элементов, выбранных из данных п элементов в произвольном порядкс, таким обрхзом два различных сочегания различаются только составом элементов.

Число всех сочеланий из п элементов по т обозначается через            и равно  п!

ПРИМЕР

Кодовый замок устроен так, что порядок набираемых цифр не важен, и каждую цифру можно использовать не более одного раза. Сколько различных четырёхзначных кодов поддерживает угот замок?

Решение

Число таких кодов равно

10! 6!.7-8-9.lO 7-9-10

= 7-3.lO=210.

                            4!.6! - 1-2-3-4-6!        з

Определение. Размещением с повторениями из п элементов по т называешя набор из т элементов, капыЙ из которых независимо выбран из исходных п элементов. Если исходные п элементов рассматривать как некий алфавит, 10 размещением с повторениями будет какое-то слово длины т.

Число всех таких размещений с повторениями обозначаепся через Rn^m рав-

НО пт.

ПРИМЕР

Сколько различных трехбуквенных слов можно составить из букв (1, [З и у?

7

Решение

Число таких слов равно = 3³ = 27.

Воспользуемся лими комбинаторными формулами и классическим определением вероятности, чтобы решить следующие задачи.

ПРИМЕР 1

Испьг.ание состоит в броске двух симметричных монеток. Какова вероят-

ПОСIЪ того, что выпадет два «орла»?

Решение

Определим множество элементарных исходов. Очевидно, что каждая монеска может выпасть «орлом» либо «решкой». Значит, возможны три варианта: два «орла», две «решки» и один «орел» и одна «решка». Являются ли эти три вариацта равновероятными (как это требуется от элементарных исходов)? Ор вет на лот вопрос зависит от того, считаем ли мы монетки различимыми или

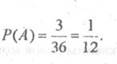нет, т.е. можем ли мы определить, какая из них первая, а какая вторая, или пе можем. Во втором случае мы имеем три элементарных исхода («орел-орёл», «орел-решка» и «решка-решка»), а в первом — четыре («орёл-орёл», «орелрешка», «решка-орёл» и «решка-решка»). В обоих случаях благоприятный для нас исход один: «орёл-орёл». По классическому определению вероятности, в первом случае ответ составит 1/4, а во втором — 1 В. Какая вероятностная модель будет верной, т.е. какое значение вероятности ближе к закономерной частоте появления интересуощего нас события? Можно, конечно, провести сатгнстический эксперимент, проведя серию таких испьггапий, и проверить, к какому отвиу будет ближе частота появления интересующего нас исхода. Опыт показывает, что любые макрообъекты (которые «можно потрогать руками») следует считать различимыми (чем мы будем всегда пользоваться в дальнейшем), и, еледовательно, нам подходит только влорая модель. Итак, ответ: 1/4,

ПРИМЕР 2

Бросаются две симметричные игральные кости. Какова вероятность собылия А, заключающегося в том, что сумма выпавших очков строго больше О?

Решение

Опишем множество элементарных исходов. На каждой кости может выпасть от 1 до 6 очков. По основному закону комбинаторики, число элементарпых исходов будет равно п = 36. Подсчитаем теперь число блатоприятных исходов. Если на первой кости выпадет меньше 5 очков, то сумма никак не сможет превысить 10. То же самое со второй костью. Причём, если выпадет 5-5, то сумма опять же будет не больше 10. Таким образом, нас устраивают три исхода: 5-6, 6-5 и 6-6, т.е. т = З. Итак, по классическому определению вероятно-

8

ПРИМЕР З

В преферанс играют втроём колодоЙ из 32 карт (в каждоЙ из четырех мастей по 8 кат от семёрки до луза). Каждому игроку разлается по 10 карт и две карты кладут в прикуп. Игрок, заказавший игру, к своим каргам добавлясг прикуп. Какова вероятность лого, что первому игроку буде;г• роздана комбинация «преферанс», т.е. у нет на pVkax будут (вместе с прикупом) дамы, короли и лузы в каждой масти?

Решение

) [о правилам игры, на руках у первого игрока вмссге с прикупом будет 12 карт из 32 карт в колоде. Таким образом, число всех элемешарных исходов равно С. 32 , а благоприятный из них только один. Таким образом искомая вероятность равна

ПРИМЕР 4

В ящике на,хощпся белых шаров и М черных. Испытание состоит в одновремснном вынимании п+т шаров ящика, nSN, пКЛ4. Какова вероятность лох), что вынуто ровно п белых шаров и т чёрных?

Решение

Всего в ящике находится ЛГ+М шаров, так что вытащить п-оп можно (.'Т+^Тм способами. Итак, чисЛ0 всех исходов равно Сл, + м . Подсчитаем число Олтоприятных исходов. Всего белых шаров N, так что вытащить из них п можпо СК, различными способами. Аналогично, т чёрных шаров можно вытащить

С.: различными способами. Итого, искомая вероятность определяется по следующей формуле:

Заметим. что формулу, полученную при решении последнего примера, мото обобщил на произвольное число типов выбираемых объектов. Если в ящике находятся М объемов первот типа, М объектов К-того типа, то вероятносљ вытянуть ровно п, объектов первого типа, объектов К-того типа

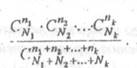
9