Построение эпюр поперечных сил изгибающих моментов и выбор сечения балок

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

Кафедра Теоретической механики

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2

По дисциплине: _______Сопротивление материалов________________________________

_____________________________________________________________________________

^{(наименование учебной дисциплины согласно учебному плану)}

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Тема:

____Построение эпюр поперечных сил изгибающих моментов и выбор сечения балок___

Автор: студент гр.   ГГ-01       ________________                  /Кузнецов А.А./

                                                                ^{(подпись)                                 (Ф.И.О.)}

Исходные данные: вариант №13

ОЦЕНКА:     _____________

Дата: ___________________

ПРОВЕРИЛ

Руководитель:          доцент.                     ________________               /Яковлев А.А./

                                  ^{(должность)                                                                 (подпись)                                                                 (Ф.И.О.)}

Санкт-Петербург

2003

                                                            Задание №1

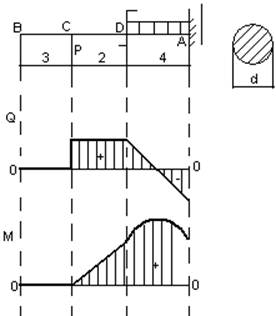                                                                                    Дано:

                                                                       

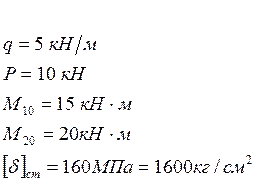
1)  Построение эпюры поперечных сил (разбиваем балку на участки и используем метод сечений):

1 уч. ВС; 3 ³ x₁ ³ 0

Q=0

Эпюра-прямая линия

2 уч. СD; 5 ³ x₂ ³ 3

Q=P=20 кН.

Эпюра –прямая.

3 уч. DA; 9 ³ x₃ ³ 5

т. D; x₃ = 5; Q_D=P-Q(x₃-5)=20 кН.

т. A; x₃ = 9; Q_A=P-Q(x₃-5)=-20 кН.

Эпюра-наклонная прямая.

Определим реакцию в точке А:

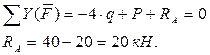
2)    Построение эпюры изгибающих моментов:

1 уч. ВС; 3 ³ x₁ ³ 0

M_B=M_C=0

Эпюра –прямая направленная по оси ОХ.

2 уч. CD; 3 ³ x₂ ³ 5

M=P(x₂-3)

т. С; x₂=3; М_С=20(3-3)=0

т. D; x₂=5; M_D=20(5-3)=40 кНм

Эпюра- наклонная прямая, направленная вверх на величину 40кНм

3 уч. DA; 9 ³ х₃ ³ 5

т. D; х₃=5; М_С= Р(х₃-3)+М-q(х₃-5)2=40+25=65 кН.

т. А; х₃=9; М_А = Р(х₃-3)+М-q(х₃-5)2=145-80=65 кН.

Эпюра – парабола, выпуклостью вверх (по правилу «зонтика»)

Определим момент, действующий в заделке:

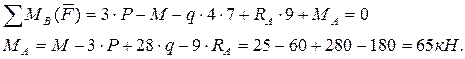
3)    Выбор поперечного сечения балки

Условия прочности для балки:

;

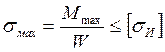- допускаемое напряжение при изгибе балки

-максимальный изгибающий момент, принимается по эпюре моментов

W- момент сопротивления сечения балки.

=65 кНм; W=162,5×10³/10⁷=16,25×10^-3 м^-3

Момент сопротивления для круглого сечения:

W=pd³/3,

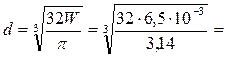40 см.

Задание №2

                                                                         

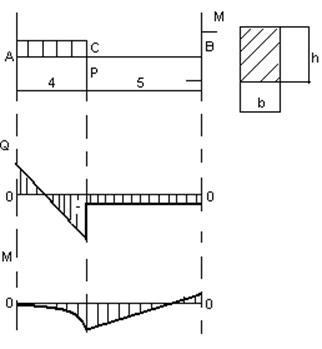
                                                                        h/b=3

                                                                        q=10 кН/м

                                                                        М=25 кНм

                                                                        Р=20 кН

1)    Определение реакций опор( составляем уравнения равновесия по правилам теормеха):

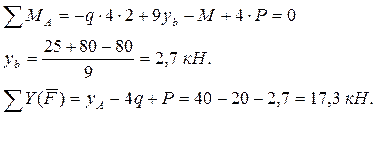
2)  Построение эпюры поперечных сил:

1 уч. АС; 4 ³ х₁ ³ 0

х₁=0; т. А ; Q_А=у_А=17,3

х₁=4; т. В; Q_B=у_А-qх₁=17,3-40=-22,7 кН.

Эпюра – наклонная прямая

2 уч. СВ; 9 ³ х₂ ³ 4

х₂=4; т. С; Q_C = у_А – 4q+P=-2,7 кН.

х₂=9; е. В; Q_C= -2,7 кН.

Эпюра – прямая, параллельная оси ОХ.

3)  Построение эпюры моментов:

АС; 1 уч.; 4 ³ х₁ ³ 0

х₁=0; т. А; М_А= 0

х₂=4; т. С; М_С= у_Ах₁ – q8 = 17,3×4-80=-10,8 кНм

Эпюра – парабола, выпуклостью вверх.

СВ; 2 уч.; 9 ³ х₂ ³ 4

х₂=4; т. С; М_С=у_Ах₂ – 4q(х₂ - 2) + Р(х₂ - 4) = 17,3×4 - 40×2=-10,8 кНм.

Х₂=9; т. В; М_В= 17,3×9 - 40×2+20×5+ М= 0,7 кНм

Эпюра- наклонная прямая.

4)  Определение сечения балки:

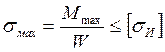=160 МПа – сталь

М_мах=10,8

W=10,8×10³/160×10⁶= 0,06×10^-3 м³

Момент сопротивления прямоугольного сечения балки:

W=bh²/6; h=3b, отсюда W=1,5b³

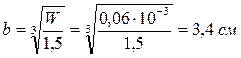
h=3*3,4=10,2 см.

Задание №3

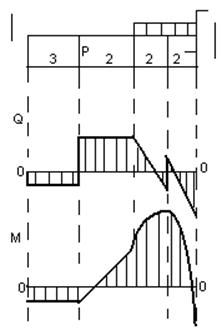
q=10 кН/м

                                                                           Р=20 кН.

                                                                           М=25 кНм.

1)     Определение реакций опор:

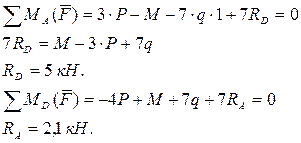
2)  Построение эпюры поперечных сил:

АВ; 1 уч; 3 ³ х₁ ³ 0

Q_A=Q_B=-R_A=-2,1

Эпюра – прямая параллельная оси балки.

ВС; 2 уч.; 5 ³ х₂ ³ 3 

Q_A=Q_B=-R_A+P=17,9 кН.

Эпюра – прямая, увеличенная на величину Р

СD; 3 уч.; 7 ³ х₃ ³ 5

Q=-R_A+P-q(x₃-5)

х₃=5; Q_C=-2,1+20=17,9 кН.

х₃=7; Q_D=-2,1+20-20=-2,1 кН

Эпюра – наклонная прямая.

DE; 4 уч.; 9 ³ х₄ ³ 7

Q=-R_A+P-2q-q(x₄-7)+R_D

x₄=7; Q_D=-2,1+20-20+5=2,9 кН.

х₄=9; Q_E=-17,1 кН

Эпюра – наклонная прямая.

3)  Построение эпюры изгибающих моментов:

АВ; 1 уч.; 3 ³ х₁ ³ 0

M_A=M_B=-R_A=-2,1 кН.

Эпюра – прямая, параллельная оси балки.

ВС; 2 уч.; 5 ³ х₂ ³ 3

х₂=3; М_В=-R_A+P(x₂-3)=-2,1 кН

x₂=5; М_С=-R_A+2P=20-2,1=17,9 кН.

Эпюра – наклонная прямая.

СD; 3 уч.; 7 ³ х₃ ³ 5

М_С=-R_A+P(x₃-3)-q(x₃-5)

х₃=5; М_С= 17,9 кН.

х₃=7; М_D= -2,1+80-20=57,9 кН.

Эпюра – парабола, выпуклостью вверх (по правилу «зонтика»)

DE; 4 уч.; 9 ³ х₄ х₃ ³ 7

х₄=7; М_D=-R_A+4P-2q=57,9 кН

х₄=9; M_E=-R_A+6P-q*4(х₄/2)+M=-37,1 кН.

Эпюра – парабола.

4)  Определение сечения балки (двутавр):

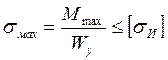=160 МПа – сталь

W=57,9×10³/160×10⁶=0,36×10^-3= 360 мм³

Проверяем двутавр на по макс. напряжению:

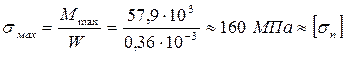
Двутавр удовлетворяет условиям.