Расчет статически неопределимых стержневых систем

Министерство образования  Российской Федерации

Санкт-Петербургский государственный  горный институт  им. Г.В. Плеханова

(технический университет)

Кафедра механики

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

	Сопротивление материалов

 

По дисциплине  __________________________________________________________

________________________________________________________________________

^{(наименование учебной дисциплины согласно учебному плану)}

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Расчет статически неопределимых стержневых систем

Тема:

________________________________________________________________________

Вариант:            №2

________________________________________________________________________

________________________________________________________________________

	ГГ-01		Кузнецов А. А.

 

Автор: студент гр.   _______    ____________________  /_________________/

                                                               ^{(подпись)                                (Ф.И.О.)}

ОЦЕНКА:     _____________

Дата: ___________________

ПРОВЕРИЛ

			.

 

Руководитель проекта   ________   ________________  /________________/

                                             ^{(должность)                (подпись)                                                   (Ф.И.О.)}

Санкт-Петербург

2003

1. Основные требования к выполнению расчетно-графического задания

Целью настоящего задания является расчет одного из предлагаемых вариантов статически неопределимой системы в условиях работы составляющих ее элементов в режиме растяжения - сжатия (одноосное напряженное состояние).

В качестве условий нагружения выбраны:

1.  нагружение внешней силы;

2.  монтажные напряжения, вызванные неточностью изготовления длины стержня, d;

3.  температурные напряжения, вызванные изменением температуры одного или нескольких стержней системы на величину DТ.

Необходимо:

a)  рассчитать площади поперечных сечений стержней системы с учетом   перечисленных выше нагрузок исходя из условий прочности;

b)  определить величины осевых усилий и напряжений в стержнях системы и построить их эпюры;

c)  произвести оценку влияния каждого из нагруженных факторов на величины и характер распределения внутренних усилий в стержнях.

2. Порядок выполнения задания:

1)  составить уравнения статики для заданной системы;

2)  определить степень статической неопределенности системы;

3)  построить схему перемещений системы;

4)  составить уравнения совместимости деформаций;

5)  выразить уравнения совместимости деформаций через усилия или напряжения, используя закон Гука;

6)  решить систему уравнений статики и совместимости деформаций относительно усилий (напряжений);

7)  исходя из условий прочности, подобрать величины площадей элементов системы при заданном соотношении площадей элементов

3. Условия задачи

Рассчитываемая  система представляет собой стержневую конструкцию с одной шарнирной опорой и двумя деформируемыми тягами (см. рис.1).

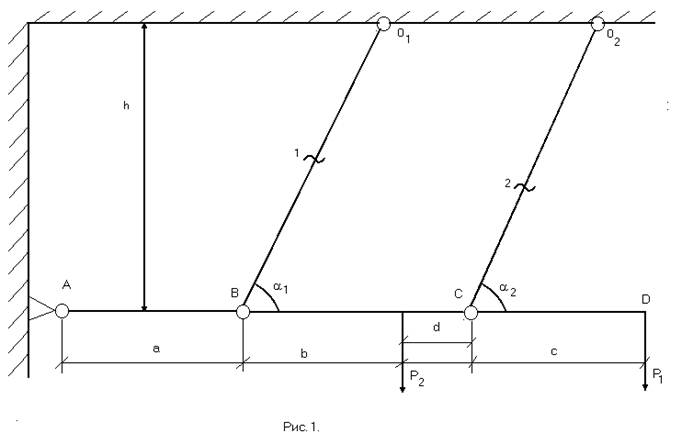
рис.1 Схема стержневой конструкции

Заданы материалы стержней: стержень один – сталь, два - медь; упругие модули на растяжение (сжатие): Е₁ = 2*10⁵ Мпа, Е₂ = 10⁵ Мпа; внешние силы Р₁ =0 Н, Р₂ = 4*10^-4 Н; коэффициенты линейного расширения материалов стержней a₁^t = 12*10⁶ , a₂^t =  16*10⁶ °C^-1.

Неточность изготовления элемента системы: стержень 2 изготовлен длиннее на величину d₂ = 0,0005*l₂.

Изменения температуры для второго стержня DТ = 20 °С.

Допустимые напряжения для материалов стержней: [s]₁ = 160 Мпа, [s]₂ = 100 Мпа.

Конструкционные соотношения площадей стержней F₂/F₁ = 2

Геометрические размеры: а = 1 м;  b = 1,8 м; c = 1 м; d = 0.5 м; h =2 м; a₁ = 45°; a₂ = 60°.

Определить величины F₂, F₁ учитывая, что балка АD (рис.1) предполагается абсолютно жесткой и невесомой.

4. Решение задачи

1. Определение усилий от внешних сил Р₁ и Р₂ (DТ = 0, d = 0)

Вычертим расчетную схему балки с указанием всех размеров и укажем внутренние силы реакций R₁  и R₂ (рис.2).

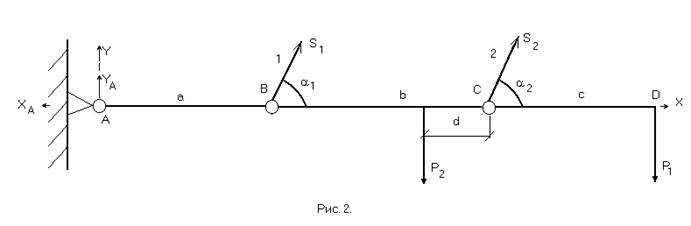
Составим уравнения статики:

                  åM_A = -R₁×a×sina₁ + P₂(a + b - d) - R₂ (a + b)sina₂ + P₁(a + b + c) = 0                (1) 

Отсюда:

                  R₁×a×sina₁ + R₂ (a + b)sina₂ =  P₁(a + b + c) + P₂(a + b - d)                                  (2)

Остальные уравнения статики можно не составлять, так как они необходимы лишь при определении реакций в шарнире Х_А, У_А, чего не требуется по условию задачи. Таким образом, степень статической неопределимости системы К=1, так как мы имеем две неизвестных реакции R₁, R₂ и одно уравнение равновесия статики (2).

Для составления одного уравнения совместимости деформаций необходимо рассмотреть схему перемещений системы (деформаций) (рис.3).  Под действием внешних сил Р₁ и Р₂ первый стержень удлиняется на величину Dl₁, а второй – на величину Dl₂, при этом жесткая балка АD повернется в положение АD₁.

              

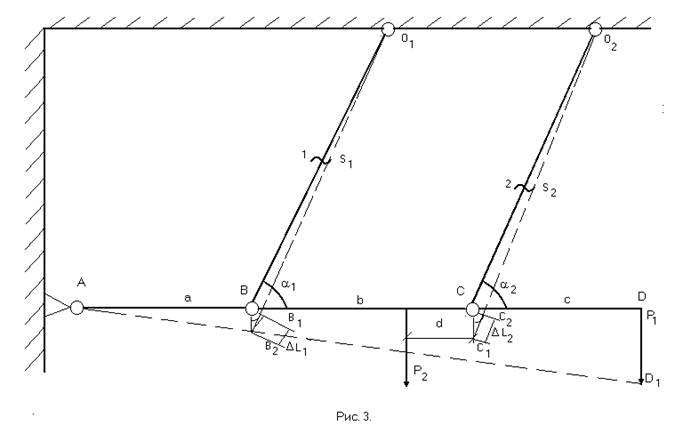
Уравнения совместности деформаций в данном случае проще всего составить, воспользовавшись подобием треугольников АВВ₁ и АСС₁:

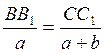                                                              (3)

Из треугольников ВВ₁В₂ и СС₁С₂ (рис.3) определим:

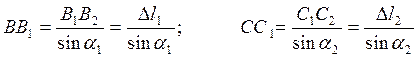                           (4)

Подставим равенства (4) в (3):

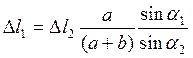                                                        (5)

Обозначим:

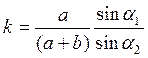                                                                             (6)

Тогда формула (5) примет вид

                                                                 (7)

Найдем деформации, используя закон Гука:

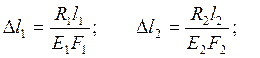
Подставляя найденные алгебраические выражения для деформаций в формулу (7) получим:

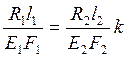
Учитывая что :

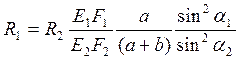                                                 (8)

Далее, решая совместно систему уравнений (8) и (2), получим:

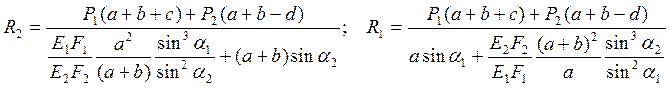   (9)

Отсюда, если учесть что  F₂/F₁ = 2, то получим такие выражения:

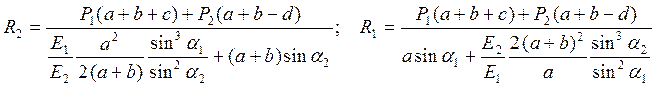         (10)

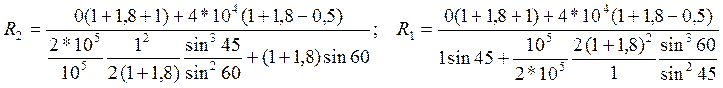
Далее, подставляя все известные значения величин из условий задачи, получим:

                                    R₁ = 7,11×10⁴ H (сжатие), R₂ = 1,69×10⁴ H (сжатие)              (11)

Проверка правильности найденных численных значений производится путем подстановки значений (11) в уравнение равновесия  (1):

-5,02×10⁴ + 9,2×10⁴ –  4,01×10⁴ @0

2.  Определение напряжений, вызванных неточностью изготовления (P=0, DT=0, d¹0)

Пусть первый стержень изготовлен с неточностью по длине d₁, а второй – с неточностью d₂, т.е. с фактической длиной несколько большей номинальной. Тогда при сборке в них появятся внутренние напряжения. Расчетная схема при этом будет выглядеть так, как показано на рис.4.

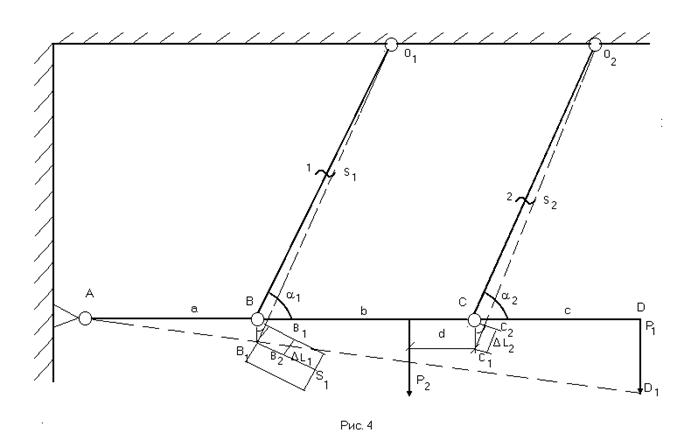
Уравнение равновесия для рассматриваемого случая будет иметь следующий вид:

                                         (12)

Для перемещений (рис.4) получим:

                               (13)

Соотношение между D₁ и D₂ находим аналогично пункту 1. (см. уравнение - (7))

                                                                     (14)

Подставив выражения (13) в равенство (14), получим уравнение совместимости деформаций в таком виде:

                                                             (15)

Где, по закону Гука :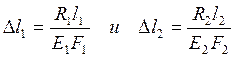

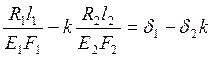                                                      (16)

Так как 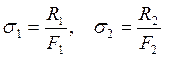 уравнение (16) можно переписать в таком виде:

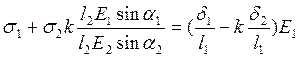                                     (17)

Перепишем уравнение (12) в напряжениях:

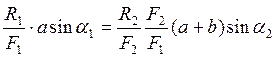
или

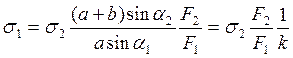                                      (18)

Далее решаем систему из уравнений (17) и (18) относительно напряжений:

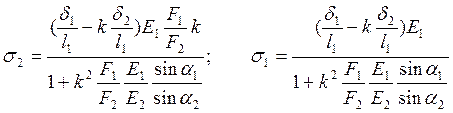                  (19)

Подставляя все значения из условия задачи, и сосчитав коэффициент k по формуле 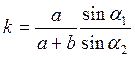, получим:

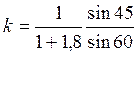
k = 0,292

s₁= 128,1 МПа 

s₂= 14,6 МПа

По полученным данным можно сказать, что оба стержня растягиваются.

3.  Расчет температурных напряжений

Предположим, что оба стержня системы нагреты до температуры Т_к +DТ, где Т_к – комнатная температура. Тогда их длины получат соответствующие приращения:

                                            (20)

Эти приращения можно формально рассматривать как неточности изготовления стержней и воспользоваться для определения возникающих при этом температурных напряжений результатами решения пункта 2 (см. уравнения (19)), заменив в окончательных выражениях . Тогда для температурных напряжений   будут справедливы соотношения:

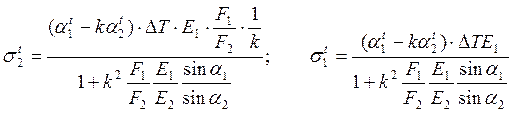                              (21)

При  и заданных геометрических и физических параметрах системы из уравнений (21) получим:

4.  Подбор сечений элементов системы

При расчете сечений учитывается одновременное действие всех нагружающих факторов: внешней нагрузки, внутренних монтажных и температурных напряжений. Полученные в пунктах 1, 2, 3 данные представим в виде таблицы 1.

Таблица №1

Действие всех нагружающих факторов

Внутренние усилия от силы Р	Напряжения, МПа			F1/F2
	от d	от DТ	допустимые
R1= 7,11*104 H	s1= 128,1 МПа		[s]1 =160 МПа
R2 = 1,69*104 H	s2=14,6 МПа		[s]2 =100 МПа

Условия прочности для каждого из стержней записывается в виде неравенств:

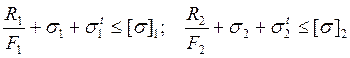                           (22)

Отсюда:

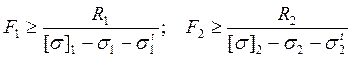                                                  (23)

Подставляя значения известных величин из таблицы 1, получим:

                                   (24)

Учитывая заданное соотношение F₂=3F₁ находим площади стержней:

Из неравенства (24) удовлетворяет =3,2*10^-4 м², при значениях =3,4*10^-4 м² неравенство не выполняется.

Окончательно выбираем: