Моделирование радиальных распределений деформаций и напряжений в сферической взрывной камере при испытании взрывчатых веществ

Работа №5. Моделирование радиальных распределений деформаций и напряжений в сферической взрывной камере при испытании взрывчатых веществ

I. Цель работы:

Научиться записывать уравнение равновесия и моделировать распределение деформаций и напряжений для  тела, имеющего сферическую симметрию.

II. Задание и порядок выполнения

Во взрывной камере проводится испытание ВВ. Взрывная камера имеет форму шара с внутренним радиусом R₁ = 0,4 м и внешним – R₂ = 0,5 м.

Рассчитать радиальные распределения деформации s_rr(R) и напряжения u_rr(R) материала камеры, если модуль Юнга E = 10⁹ Па, коэффициент Пуассона s = 0,35. Давление внутри камеры p₁ = 10⁷ Па, снаружи – p₂ = 10⁵ Па.

            1. Определите явный вид функции деформации u(R).

В сферических координатах уравнение равновесия камеры имеет вид

            Отсюда, 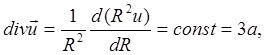следовательно, можно записать  и, интегрируя, определить явный вид функции.

            2. Определите аналитический вид компонентов тензора деформации

по формулам 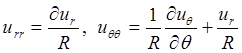 где u_rr(R) и u_qq(R) – радиальные и угловые деформации, соответственно.

            3. Определите постоянные интегрирования по п. 1 a и b.

            Радиальное напряжение дается формулой

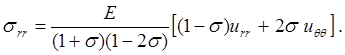
Постоянные a и b находятся из граничных условий

            4. Постройте графики радиальных распределений и деформаций.

III. Пример оформления

               Для тензора деформаций имеем 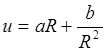, отсюда

» syms a b R;

» diff('a*R+b/R^2',R)

ans =

a-2*b/R^3

»

.

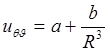Примерный вид файла, содержащего текст сценария для определения постоянных интегрирования a и b и построения графика:

E = 1e9; sigma = 0.35; R1 = 0.4; R2 = 0.5; P1 = 1e7; P2 = 1e5;

C1 = E/((1+sigma)*(1-2*sigma));

C2 = C1*(1-sigma);

C3 = C1*2*sigma;

% sigma_rr = (C2+C3)*a + (C3-2*C2)/R^2*b

C4 = C2+C3; C5 = C3-2*C2;

% sigma_rr = C4*a + C5/R^2*b

% решаем матричное уравнение Ax = B

A = [C4,C5/R1^2;C4,C5/R2^2];

B = [P1;P2];

X = A \ B;

a = X(1);

b = X(2);

R = R1:0.01:R2;

sigma_rr = C4*a + C5./R.^2*b;

plot(R,sigma_rr);

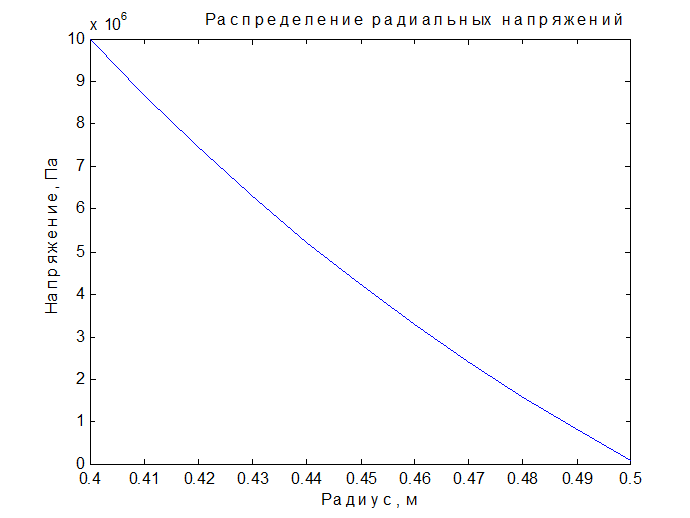
title('Распределение радиальных напряжений');

xlabel('Радиус, м');

ylabel('Напряжение, Па')

   Результаты работы системы MatLab