Рассмотрим некоторые конкретные законы распределения случайных величин, имеющих плотность вероятности.
Закон равномерной плотности.
Предположим, что о некоторой случайной величине x заранее известно, что она попадает в
определенный интервал оси Ox [a,b], причем все значения x в этом интервале одинаково вероятны
(обладают одной и той же плотностью вероятности, f(x) = const). Тогда
говорят, что случайная величина x
распределена по закону равномерной плотности: 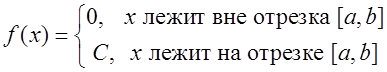
Постоянная С определяется из условия нормировки: 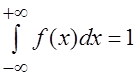 откуда получаем уравнение:
откуда получаем уравнение: 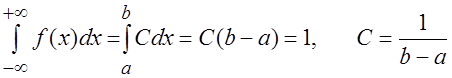 . Итак, равномерная плотность имеет вид:
. Итак, равномерная плотность имеет вид: 
Это двухпараметрическое распределение с двумя параметрами a и b
Нарисуем график такой плотности вероятности.
Легко строится функция распределения F(x):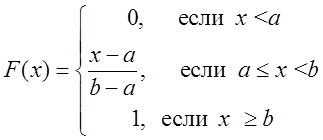
Функция распределения F(x) имеет кусочно-линейный вид.
Нарисуем ее график. Функция распределения F(x) позволяет вычислять вероятности попадания равномерно распределенной случайной величины x в тот или иной интервал числовой оси Ox.
Найдем математическое ожидание ![]() . Имеем
. Имеем 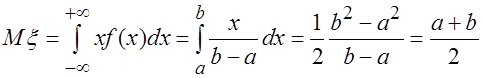
Медиана ![]() равномерного
распределения равна этой же величине:
равномерного
распределения равна этой же величине:
Найдем дисперсию равномерного 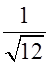 распределения:
распределения: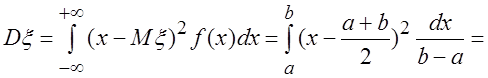
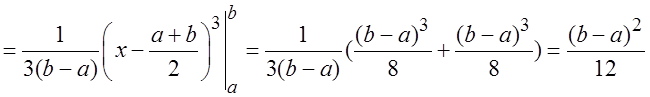
Итак, для равномерного распределения дисперсия 
Можно еще рассмотреть стандартно распределенную равномерную случайную величину x. Для нее a=0, b=1. Следовательно, эта величина равномерно распределена на отрезке [0,1]. Математическое ожидание такой величины равно 0.5, а дисперсия равна.
Стандартная случайная величина x, равномерно распределенная на отрезке [0,1], наиболее часто применяется в различных теоретико-вероятностных расчетах.
Нормальный закон распределения.
Случайная величина x
называется распределенной по нормальному закону, если ее плотность вероятности f(x) имеет вид: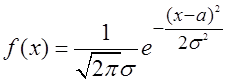 . Другое употребительное название такой
плотности – гауссова функция ошибок. Коротко записывают еще и так:
. Другое употребительное название такой
плотности – гауссова функция ошибок. Коротко записывают еще и так: ![]() Это означает, что плотность вероятности
случайной величины x имеет вид:
Это означает, что плотность вероятности
случайной величины x имеет вид: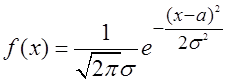 .Это двухпараметрическое распределение, с
двумя параметрами: a и s.Для этой плотности, величина s
должна быть положительной, иначе функция f(x) окажется отрицательной и не сможет быть плотностью
вероятности. Аналогичного ограничения на величину a наложить нельзя, она пока может быть произвольной. Для
более полного уточнения условий, которые надо наложить на оба эти параметра,
рассмотрим выполнение условия нормировки плотности:
.Это двухпараметрическое распределение, с
двумя параметрами: a и s.Для этой плотности, величина s
должна быть положительной, иначе функция f(x) окажется отрицательной и не сможет быть плотностью
вероятности. Аналогичного ограничения на величину a наложить нельзя, она пока может быть произвольной. Для
более полного уточнения условий, которые надо наложить на оба эти параметра,
рассмотрим выполнение условия нормировки плотности: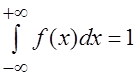 ?
Имеем в случае нормального закона
?
Имеем в случае нормального закона 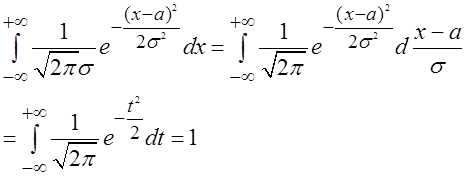
Условие нормировки выполнено, причем никаких других ограничений на величины s и a накладывать не надо, плотность нормального закона будет автоматически нормированной при s > 0, a - любая конечная величина.
Найдем математическое ожидание и дисперсию нормально распределенной случайной величины x.
Имеем 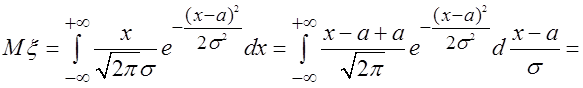
=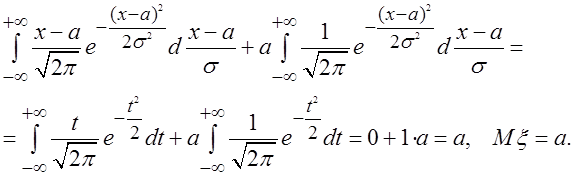
Оказывается, параметр распределения a в нормальном законе означает математическое ожидание случайной величины.
Для дисперсии: 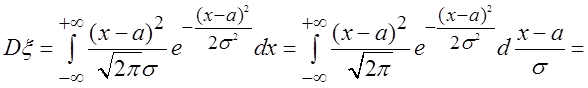
=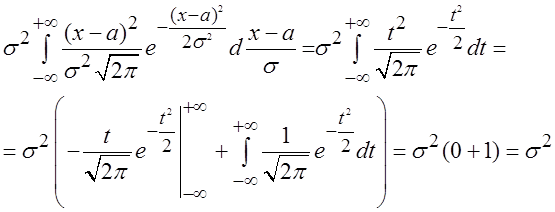
![]() .
.
Дисперсия нормального закона распределения оказалась равной
другому параметру распределения: ![]() . Следовательно,
параметр s является среднеквадратичным
отклонением для нормально распределенной случайной величины x.
. Следовательно,
параметр s является среднеквадратичным
отклонением для нормально распределенной случайной величины x.
В частном случае, когда a = 0, s =s2 =1, получаем плотность так
называемого стандартного нормального закона с плотностью вероятности 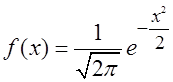 . Нарисуем график функции
. Нарисуем график функции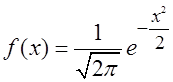 (шапочка), отметим точку экстремума и две
точки перегиба с абсциссами x=±1. Говоря другими словами, точка перегиба
стандартной плотности нормального закона находится на расстоянии от оси Oy, равном единице, то есть равном среднеквадратичному
отклонению s = 1.
(шапочка), отметим точку экстремума и две
точки перегиба с абсциссами x=±1. Говоря другими словами, точка перегиба
стандартной плотности нормального закона находится на расстоянии от оси Oy, равном единице, то есть равном среднеквадратичному
отклонению s = 1.
График плотности вероятности в общем случае (при
произвольных a и s), то есть график функции 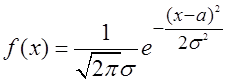 выглядит аналогично: это «шапочка» с точкой
максимума при x=a и двумя точками перегиба при x
= a- s
и x= a+ s. Можно сказать так, что расстояние между
точками перегиба на графике нормальной плотности вероятности равно удвоенному
среднеквадратичному отклонению 2s. Это
свойство позволяет иногда находить среднеквадратичное отклонение s в нормальном законе геометрическим методом,
находя расстояние между точками перегиба на графике плотности вероятности, и
приравнивая его 2s, находить само s.
выглядит аналогично: это «шапочка» с точкой
максимума при x=a и двумя точками перегиба при x
= a- s
и x= a+ s. Можно сказать так, что расстояние между
точками перегиба на графике нормальной плотности вероятности равно удвоенному
среднеквадратичному отклонению 2s. Это
свойство позволяет иногда находить среднеквадратичное отклонение s в нормальном законе геометрическим методом,
находя расстояние между точками перегиба на графике плотности вероятности, и
приравнивая его 2s, находить само s.
Рассмотрим теперь функцию распределения F(x) для нормального закона. Имеем по определению 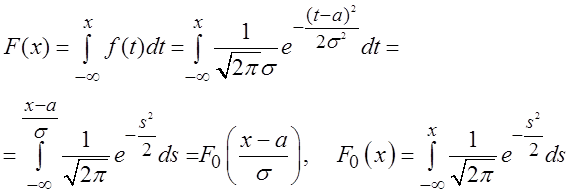
Итак, функция распределения нормального закона F(x) выражается через
вспомогательную функцию F0(x): 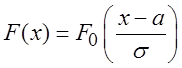 , причем фактически
функция F0(x)
является функцией распределения стандартного нормального закона с математическим
ожиданием 0 и дисперсией, равной 1.
, причем фактически
функция F0(x)
является функцией распределения стандартного нормального закона с математическим
ожиданием 0 и дисперсией, равной 1.
Функция F0(x) табулирована и приводится во многих учебниках и математических монографиях по теории вероятностей и математической статистике.
В некоторых случаях вместо функции распределения F0(x) используется
функция Лапласа 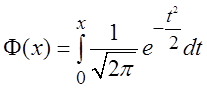 . Можно видеть, что имеет место
равенство:
. Можно видеть, что имеет место
равенство: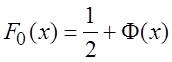 . Функция Лапласа Ф(x) является нечетной функцией аргумента x, поэтому ее табулируют только на полуинтервале от x = 0 и до x= +¥ (обычно – до x=5).
. Функция Лапласа Ф(x) является нечетной функцией аргумента x, поэтому ее табулируют только на полуинтервале от x = 0 и до x= +¥ (обычно – до x=5).
Выразим вероятность произвольного случайного события,
связанного с нормально распределенной случайной величиной, через функцию
Лапласа:
Пример. Правили «трех сигм» для нормально распределенной случайной величины.
Рассмотрим вероятность случайного события
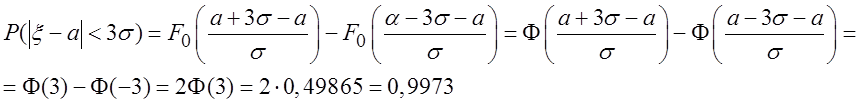 Получается, что нормально распределенная
случайная величина с большой вероятностью 0,9973 попадает в интервал шириной 6s, центром которого является математическое
ожидание a, а во внешность этого интервала
попадает с вероятностью 0,0073. Эта вероятность сама по себе очень мала,
она значительно меньше
Получается, что нормально распределенная
случайная величина с большой вероятностью 0,9973 попадает в интервал шириной 6s, центром которого является математическое
ожидание a, а во внешность этого интервала
попадает с вероятностью 0,0073. Эта вероятность сама по себе очень мала,
она значительно меньше ![]() , как это имело место
в неравенстве Чебышева для произвольной случайной величины, имеющей конечную
дисперсию. Появление дополнительной информации о случайной величине (о том, что
случайная величина x нормально
распределена) существенно суживает интервал «правила трех сигм».
, как это имело место
в неравенстве Чебышева для произвольной случайной величины, имеющей конечную
дисперсию. Появление дополнительной информации о случайной величине (о том, что
случайная величина x нормально
распределена) существенно суживает интервал «правила трех сигм».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.