Построение интегральной кривой стока в прямоугольной и косоугольной системах координат по среднемесячным расходам реки Иня. Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Чулым

Санкт-Петербургский Государственный Политехнический Университет

Инженерно-строительный факультет

Кафедра «Инженерных мелиораций, гидрологии и охраны окружающей среды»

Курсовая работа по инженерной гидрологии

Выполнил: Шепетько В.В. 

группа 3013/1

               Проверил: Скворцова О.С.

Санкт-Петербург

-2011-

Оглавление

1. Построение интегральной кривой стока в прямоугольной и   косоугольной системах координат по среднемесячным расходам реки Иня.. 4

2. Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Чулым... 11

3. Построение математической и эмпирической кривых обеспеченности максимальных годовых расходов реки Чулым... 14

4. Вычисление коэффициента корреляции между максимальными наблюденными расходами рек Иня и Чулым. Метод линейной корреляции.. 18

Литература.. 22

1. Построение интегральной кривой стока в прямоугольной и косоугольной системах координат по среднемесячным расходам реки Иня

Основными гидрологическими характеристиками реки являются: отметка уровня водной поверхности  , скорость течения воды в реке υ, площадь живого сечения ω, расход воды Q, сток W.

Расход Q – это количество воды, проходящей через живое сечение реки в единицу времени.

Сток W – это то количество воды, которое прошло с начала измерений за любой промежуток времени.

Наряду с этими характеристиками важной характеристикой реки является ее гидрограф, дающий представление об изменении расходов воды во времени для данного створа реки.

Створ – это плоскость, проходящая через реку так, чтобы она была ортогональна скорости течения.

Гидрограф строится по данным водомерных постов. По гидрографу можно определить тип реки, вид ее питания. На рис.1 представлен гидрограф, характерный для равнинных рек.

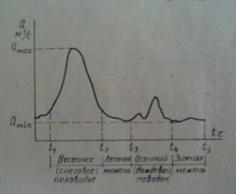
Рис.1. Гидрограф равнинных рек

Однако для гидрологических расчетов одного гидрографа недостаточно. Например, определить количество воды, которое прошло через данный створ за какой-либо промежуток времени по гидрографу затруднительно. Поэтому в таких случаях используют интегральную кривую (кривую стока), характеризующая сток реки. Интегральная кривая строиться либо в прямоугольной, либо в косоугольной системе координат.

Интегральная кривая стока в прямоугольной системе координат

Если бы функция Q=f(t) была задана, то, интегрируя ее, можно получить значение стока за промежуток времени t₂ – t₁:

 .

Но поскольку вид функции неизвестен, то величина стока определяется обычно методом графического интегрирования (методом прямоугольников). Элементарный сток за промежуток времени Δt_i равен (рис.2):

 ,

а сток за время t_i=n·Δt_i равен сумме n элементарных столбцов, то есть:

 ,

(если Δt_i равно одному месяцу, а  – среднемесячный расход, то в этом случае n – число месяцев; если Δt_i равно одному дню, а  – среднесуточный расход, то n –число дней и т.д.).

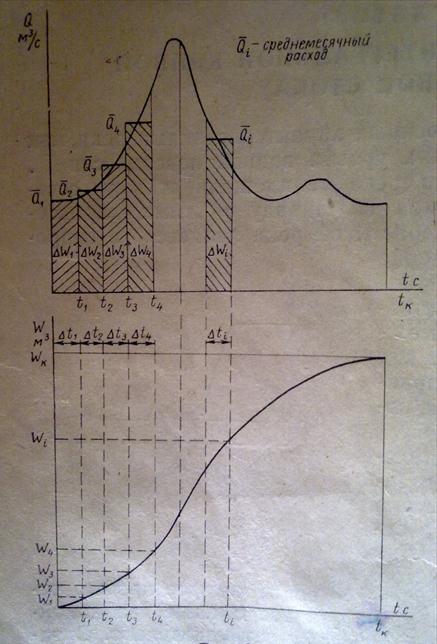
Рис.2. Построение интегральной кривой стока по гидрографу

Свойства интегральной кривой стока:

1. Интегральная кривая стока всегда возрастает.

      Если линия параллельна оси времени, следовательно, расход реки равен нулю,      

      следовательно, река высохла.

2. Перегибы на интегральной кривой стока соответствуют экстремуму ни гидрографе.
3. Зарегулированная река – это водоток, который в любой момент времени поддерживает   постоянный расход. Утром и вечером расход реки больше, чем днём и ночью.

4.   Тангенс угла наклона прямой, соединяющей начало и конец интегральной кривой стока,      

      пропорционален среднему многолетнему расходу.

Выбор масштаба для построения интегральной кривой стока:

Допусти, что масштаб стока уже выбран, то есть известен масштабный коэффициент m_w – количество единиц стока в одном сантиметре чертежа (м³/см). Пусть известен масштаб времени m_t – количество единиц времени в 1см чертежа (с/мес·см). Пусть также выбранный масштаб расхода есть m_Q – количество единиц расхода в 1см чертежа (м³/с·см). Соответствующую величину отрезка, измеренную на чертеже, обозначаем в квадратных скобках, например W=[W]·m_w, где [W] – отрезок на чертеже, выраженный в единицах длины (см), измеренный по оси W. Тогда:

tg α_i = [W_i] / [t_i], или

tg α_i = (W_i / m_w) / (t_i / m_t) = (W_i / t_i) · (m_t / m_w) = Q_i · (m_t / m_w).

Затем восстанавливаем перпендикуляр к горизонтальному «нулевому» лучу, откладываем на этой вертикали (оси Q) в выбранном масштабе «удобный» для интерполяции расход Q₀ и далее 2Q₀, 3Q₀ и т.д. Определяем далее длину отрезка [Q_i], отвечающего расходу Q_i: [Q_i] = Q_i / m_Q, и откладываем его на оси Q (см. рис.4). Проводим из точки, соответствующей расходу Q_i, луч под углом α_i к горизонтальной линии и находим тем самым в точке их пересечения полюс лучевого масштаба О и полюсное расстояние Р. Аналитическое выражение для Р получается, если воспользоваться следующей зависимостью:

tg α_i = [Q_i] / P = Q_i / m_Q·P.

Приняв два последних выражения, имеем:

P = m_w/m_Q·mt.

Имея такой масштаб, можно легко найти расход в любой точке суммарной кривой.

График интегральной кривой стока в прямоугольной системе координат представлен на рис.4. Там же указаны масштабы и масштабные коэффициенты, выбранные для построения графика, а также формулы для определения tg α и полюсного расстояния ОР.

M_w   в 1см 2·10⁹м³,

M_Q   в 1см 100м³/с,

M_t    в 1см 1мес (2,63·10⁶с),

m_w = 2·10⁹м³/см,

m_Q = 100м³/с·см,

m_t = 2,63·10⁶с/мес·см.

tg α = 509,85м³/с · (2,63·10⁶с/мес·см / 2·10⁹м³/см) = 0,67.

ОР = 2·10⁹м³/см / (100м³/с·см · 2,63·10⁶с/мес·см) = 7,6см.

Интегральная кривая стока в косоугольной системе координат

Использование кривой W=φ(t), построенной в прямоугольной системе координат, не совсем удобно, если имеется несколько лет наблюдений или значения стока велики. Кривая в этом случае растет вверх и в длину. Суммарная кривая имеет более компактный вид в косоугольной системе координат, особенно в том случае, если в качестве одной из осей использовать прямую, которой в прямоугольной системе координат соответствует средний многолетний расход (прямая ОА на рис.3 ). Преобразование координат легко представить, если мысленно повернуть прямую ОА на угол α₀ по часовой стрелке так, чтобы точка А совместилась с точкой А’ (см. рис.3). При этом ось времени тоже повернётся на угол α₀.

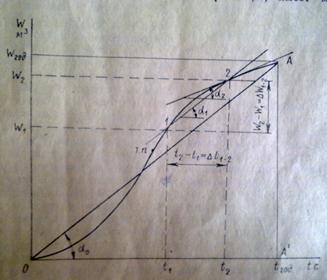
Рис.3. Интегральная кривая стока в прямоугольной системе координат

График интегральной кривой стока в косоугольной системе координат представлен на рис.5. Там же указаны масштабы и масштабные коэффициенты, выбранные для построения графика, а также формулы для определения tg α₀ и полюсного расстояния ОР. В данной системе координат масштаб оси W увеличивается, вследствие чего меняется угол α и полюсное расстояние ОР.