Строительство и архитектура \ Инженерная гидрология

Построение интегральной кривой стока в прямоугольной и косоугольной системах координат по среднемесячным расходам реки Иня. Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Чулым, страница 3

Kmax K1

K1 К2

K2 К3

K3 К4

K4 К5

K4 К5

K5 К6

K6 К7

K7 К8

K9 К10

K10 К11

K11 Kmin

m

4

2

0

1

1

2

1

5

4

3

1

1

Pi, %

16

8

0

4

4

8

4

20

16

12

4

4

P, %

16

24

24

28

32

40

44

64

80

92

96

100

сглаживание

объединенные интервалы

4+2+0+1=7

1+2+1+5=9

4

3+1=4

1

число попавшихся расходов

7расх/4инт = 1,75

9расх/4инт = 2,25

4

4расх/2инт = 2

1

Р, %

7

7

7

7

9

9

9

9

16

8

8

4

Р, %

7

14

21

28

37

46

55

64

80

88

96

100

3. Построение математической и эмпирической кривых обеспеченности максимальных годовых расходов реки Чулым

Для построения эмпирической кривой обеспеченности (рис.7) воспользуемся табл.2. Для этого все данные необходимо расположить в убывающем порядке. Эмпирическая кривая обеспеченности строиться по величинам Pi и Ki.

Для построения математической кривой необходимо, прежде всего, вычислить по данным наблюдений параметры этой кривой – коэффициенты Cv и Cs:

 ,        .

 ,       .

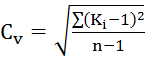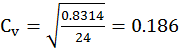Мерой погрешности принято считать среднее квадратическое отклонение (средняя квадратическая ошибка).

Относительная средняя квадратическая ошибка среднего расхода (нормы) вычисляется:

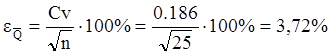
Относительная средняя квадратическая ошибка коэффициента вариации составляет:

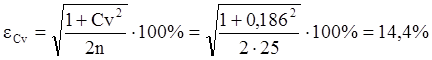
Относительная средняя квадратическая ошибка коэффициента асимметрии равна:

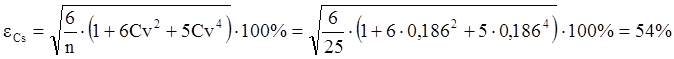
Для определения несмещенных параметров  и  воспользуемся методом моментов (поскольку ).

Для нахождения коэффициентов вариации и асимметрии воспользуемся следующими формулами:

,

.

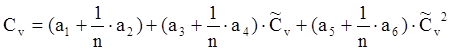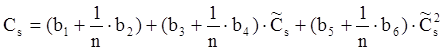Величины а и b берутся в зависимости от коэффициента автокорреляции ( r ).

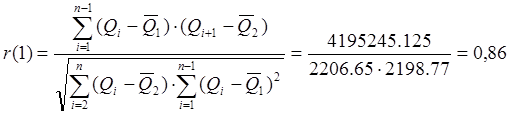
Расчет коэффициента автокорреляции представлен в табл.4.

Таблица 4

№ п/п

Qi, м3/с

Qi - Q1

Qi+1 - Q2

(Qi-Q1)(Qi+1-Q2)

(Qi-Q1)2

(Qi-Q2)2

1

3402

788

0

620813

Q1=

2614

2

3400

786

854

670779,875

617665

728462

3

3358

744

812

603688,375

553412

658532

Q2=

2547

4

3310

696

764

531332,375

484300

582932

5

3200

586

654

382896,5417

343298

427062

6

3160

546

614

334919,875

298025

376382

7

2890

276

344

94777,375

76130

117992

8

2781

167

235

39141,95833

27861,2

54990,3

9

2662

48

116

5534,375

2296,01

13340,3

10

2611

-3

65

-198,875

9,50694

4160,25

11

2500

-114

-47

5304,875

13015

2162,25

12

2458

-156

-89

13813,375

24362

7832,25

13

2450

-164

-97

15834,04167

26923,3

9312,25

14

2432

-182

-115

20848,54167

33154,3

13110,3

15

2360

-254

-187

47386,54167

64558,3

34782,3

16

2340

-274

-207

56598,20833

75121,7

42642,3

17

2335

-279

-212

59026,125

77887,5

44732,3

18

2270

-344

-277

95139,04167

118393

76452,3

19

2220

-394

-327

128668,2083

155302

106602

20

2219

-395

-328

129389,7917

156091

107256

21

2160

-454

-387

175503,2083

206192

149382

22

2150

-464

-397

184009,0417

215373

157212

23

2100

-514

-447

229538,2083

264282

199362

24

1970

-644

-577

371314,0417

414843

332352

25

1780

-767

0

587522

4195245,125

4869308

4834570

корень

2206,65

2198,77

r =

0,86

Зная коэффициент автокорреляции, определяем коэффициенты a и b (табл.5) и считаем коэффициенты  и  .

Индекс

а

b

1

0

0,03

2

0,18

1,63

3

0,98

0,92

4

0,41

-0,97

5

0,02

0,03

6

1,47

7,94

 и .

Значения для построения математической и эмпирической кривых представлены в табл.6 и табл.7.

Скачать файл