Построение интегральной кривой стока в прямоугольной и косоугольной системах координат по среднемесячным расходам реки Иня. Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Чулым, страница 4

Табл.6 Р, % Кi 1 1,49 3 1,39 5 1,33 10 1,25 20 1,15 25 1,12 30 1,09 40 1,04 50 0,99 60 0,94 70 0,90 75 0,87 80 0,84 90 0,76 95 0,71 97 0,68 99 0,61

Табл.7 Р, % Кi 1 1,52 3 1,41 5 1,35 10 1,26 20 1,16 25 1,13 30 1,09 40 1,04 50 0,99 60 0,94 70 0,89 75 0,86 80 0,83 90 0,75 95 0,69 97 0,66 99 0,59

Графики математической и эмпирической кривых обеспеченности представлены на рис.7.

4. Вычисление коэффициента корреляции между максимальными наблюденными расходами рек Иня и Чулым. Метод линейной корреляции

В данном пункте необходимо определить расчетные гидрологические характеристики при недостаточности данных наблюдений (р.Иня). При недостаточности данных, необходимо удлинить ряд наблюдений с использованием схожей реки. Основным способом удлинения ряда наблюдений является метод аналогии. Этот метод можно применить, когда есть совместные года наблюдений.

При выборе реки-аналога учитываются следующие условия:

- возможная географическая близость водосборов;

- сходство климатических условий;

- однотипность формирования стока (однотипность почв, по возможности, близкая степень озёрности, заселенности, заболоченности и распаханности);

- площади водосборов не должны отличаться более чем в 10 раз, а средние высоты водных рек не должны отличаться более чем на 30м;

- должны отсутствовать факторы, существенно влияющие на сток (река не должна быть зарегулирована, не должно быть сбросов и мелиорации);

- наличие совместных лет наблюдений не менее 10 лет.

При применении метода аналогии необходимо найти уравнение связи между гидрологическими величинами изучаемой реки и реки-аналога. В качестве него принимается линейное уравнение регрессии. Так как гидрологические величины являются случайными, связь между ними не строго функциональная.

С целью отыскания зависимости между случайными величинами используется метод прямолинейной регрессии с вычислением коэффициента корреляции, который оценивает связи между величинами.

Составим таблицу (табл.8) расходов р.Иня и р.Чулым при совместных годах наблюдений.

Таблица 8

Год		Qai		Qi	Qai-Qa’	Qi-Q’		(Qai-Qa’)2	(Qi-Q’)2	(Qai-Qa’)·(Qi-Q’)
1907		3160		1610	718	336		515524	112896	241248
1908		2335		1178	-107	-96		11449	9216	10272
1911		2340		1205	-102	-69		10404	4761	7038
1912		2458		1250	16	-24		256	576	-384
1913		2662		1562	220	288		48400	82944	63360
1922		1780		930	-662	-344		438244	118336	227728
1923		2360		1184	-82	-90		6724	8100	7380
		2442		1274				1031001	336829	556642

 Коэффициент регрессии вычисляется по следующей формуле:

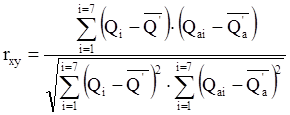
где n – число лет совместных наблюдений (n=7);

Q^’ - средний расход изучаемой реки;

Q^’_a - средний расход реки-аналога (р. Чулым);

        Q_i, Q_ai – расходы в i-ый год соответственно для изучаемой реки и реки-аналога.

Для коэффициента регрессии должно выполняться условие: r_xy ≥ 0,7.

 .

Среднеквадратическое отклонение коэффициента регрессии составляет:

 .

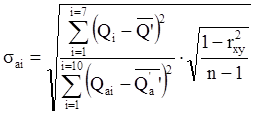
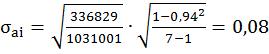Составим уравнение регрессии:

a₂ = r_xy·σ’/σ_a’

 .

 

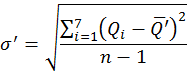
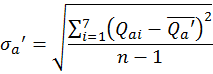
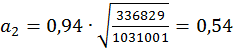a₁ = 1274 – 0,54·2442 = - 44,7.

Также для коэффициента регрессии должно выполняться еще одно условие:

 ,

 .

Q_i = - 44,7 + 0,54·Q_ai .

Согласно уравнению регрессии продлеваем ряд наблюдений (табл.9).

Таблица 9

год	1899	1900	1901	1902	1903	1904	1905	1906	1907	1908	1909	1910	1911
Qa, m3/c	2220	3200	3400	2781	2500	3402	3310	3358	3160	2335	2100	2270	2340
Qi, м3/c	1154	1683	1791	1457	1305	1792	1743	1769	1662	1216	1089	1181	1219
									1610	1178			1205
год	1912	1913	1914	1915	1916	1917	1918	1919	1920	1921	1922	1923
Qa, m3/c	2458	2662	2611	2219	1970	2150	2450	2432	2160	2890	1780	2360
Qi, м3/c	1283	1393	1365	1154	1019	1116	1278	1269	1122	1516	917	1230
	1250	1562									930	1184

График прямой регрессии представлен на рис.8 .

Литература

1.  Канарский Н.Д., Михалев М.А. Гидрологические расчеты. Учебное пособие. - Л.: ЛПИ, 1984. – 64с.

2.  Инженерная гидрология: методические указания к курсовой работе. Сост. Т.Д. Кумина, СПб.гос.техн.ун-т; 1995