Цель работы: проверка гипотезы о нормальном законе распределения статистических данных.
Краткие теоретические сведения.
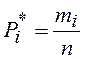 , где Pi* - относительная частота; mi – абсолютная частота попадания
параметра x в интервал; n – общее число статистических данных.
, где Pi* - относительная частота; mi – абсолютная частота попадания
параметра x в интервал; n – общее число статистических данных.
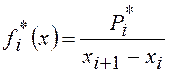 , где fi*(x) –
высота прямоугольника гистограммы.
, где fi*(x) –
высота прямоугольника гистограммы.
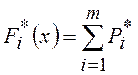 , где Fi*(x) –
высота прямоугольника кумулятивной кривой; m – число суммируемых частот до х=хi.
, где Fi*(x) –
высота прямоугольника кумулятивной кривой; m – число суммируемых частот до х=хi.
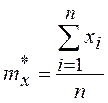 ,
,
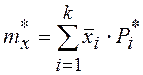 , где mx* - среднее арифметическое значение параметра.
, где mx* - среднее арифметическое значение параметра.
где k – число разрядов; ![]() - середина i-ого интервала.
- середина i-ого интервала.
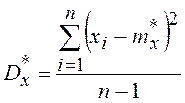 ,
,
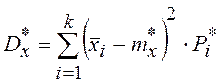 , где Dx* - статистическая дисперсия.
, где Dx* - статистическая дисперсия.
Метод моментов. При методе моментов вид теоретической кривой плотности распределения подбирается по виду гистограммы, а числовые ее характеристики (моменты) принимаются равными соответствующим статистическим характеристикам. Так, для нормального распределения mx=mx*; Dx=Dx*.
Для построения теоретической кривой плотности нормального распределения (на графике гистограммы) рассчитываются ее значения в нескольких точках, обычно соответствующих границам интервалов, по формуле
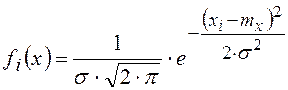 .
.
Проверяется гипотезу о нормальном законе распределения при помощи одного из критериев согласия. Наиболее распространен критерий Пирсона
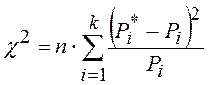 , где Pi – теоретическая вероятность
попадания параметра х в i-ый
интервал. При нормальном законе распределения
, где Pi – теоретическая вероятность
попадания параметра х в i-ый
интервал. При нормальном законе распределения
![]()
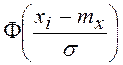 -
-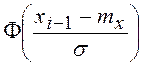 , где Ф(…) – табулированная функция
Лапласа.
, где Ф(…) – табулированная функция
Лапласа.
Гипотеза о нормальном законе распределения не противоречит статистическим данным, если χ2> χp2. Величина χp2 зависит от уровня значимости p и числа степеней свободы ν=k-m-1, где k – число интервалов; m=2.
Метод вероятностных сеток. График функции распределения F(x), представляющий собой кривую линию, соответствующим преобразованием зависимых величин делают прямолинейным. Прямоугольная сетка, на которой график функции представляет собой прямую, называется вероятностной сеткой. Для прямолинейного графика по оси абсцисс откладывают величину Sx, соответствующую значению аргумента x, а по оси ординат – величину SF, соответствующую значению функции F(x). Шкала по оси абсцисс равномерная и строится с использованием соотношений
Sx=Kx*x, Kx=L/∆x, ∆x=xmax-xmin, где L – принятая ширина графика.
Шкала по оси ординат неравномерная и строится с использованием соответствующей формулы.
После построения шкал вероятностной сетки на нее наносятся точки, соответствующие значениям функции распределения на границах интервалов. Через точки проводится прямая таким образом, чтобы наибольшие отклонения точек от проведенной прямой были минимальными. Среднее квадратичное отклонение, если длина шкалы на оси ординат равна 300 мм, рассчитывается по формуле
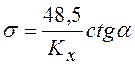 ,
,
Гипотезу о нормальном законе распределения можно принять, если все точки лежат на проведенной прямой или если величина критерия Пирсона будет малой.
Выполнение работы:
В качестве однотипных радиоэлементов использовались резисторы с номинальным сопротивлением 1 кОм, в качестве измерительного прибора использовался мультиметр.
|
973 |
||
|
941 |
||
|
994 |
||
|
977 |
||
|
993 |
||
|
978 |
||
|
978 |
||
|
995 |
||
|
1004 |
||
|
943 |
||
|
999 |
||
|
1004 |
||
|
1001 |
||
|
1010 |
||
|
988 |
||
|
993 |
||
|
992 |
||
|
986 |
||
|
983 |
||
|
1001 |
||
|
997 |
||
|
1023 |
||
|
1010 |
||
|
1002 |
||
|
990 |
||
|
993 |
||
|
981 |
||
|
1000 |
||
|
1007 |
||
|
1006 |
||
|
1010 |
||
|
992 |
||
|
982 |
||
|
986 |
||
|
996 |
||
|
1000 |
||
|
1013 |
||
|
1002 |
||
|
951 |
||
|
997 |
||
|
1001 |
||
|
985 |
||
|
1005 |
||
|
1005 |
||
|
1001 |
||
|
997 |
||
|
983 |
||
|
989 |
||
|
989 |
||
|
995 |
||
|
991 |
||
|
|
||
|
994 |
||
|
1030 |
||
|
994 |
||
|
1030 |
||
|
994 |
||
|
975 |
||
|
1001 |
||
|
1013 |
||
|
1012 |
||
|
988 |
||
|
1024 |
||
|
1003 |
||
|
989 |
||
|
991 |
||
|
997 |
||
|
1014 |
||
|
995 |
||
|
1000 |
||
|
999 |
||
|
993 |
||
|
1002 |
||
|
991 |
||
|
988 |
||
|
1005 |
||
|
1003 |
||
|
1001 |
||
|
988 |
||
|
987 |
||
|
989 |
||
|
1021 |
||
|
1001 |
||
|
996 |
||
|
994 |
||
|
984 |
||
|
1005 |
||
|
972 |
||
|
997 |
||
|
100 |
||
|
998 |
||
|
990 |
||
|
987 |
||
|
985 |
||
|
1007 |
||
|
1007 |
||
|
1003 |
||
|
996 |
||
|
990 |
||
|
992 |
||
|
980 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.