Проверка гипотезы о нормальном законе распределения статистических данных. Краткие теоретические сведения, страница 2

Интервалы	941-950	951-960	961-970	971-980	981-990	991-1000	1001-1010	1011-1020	1021-1030
Частота (Pi*)	0,02	0,01	0	0,07	0,22	0,33	0,26	0,04	0,05
Вероятность (P)	0,001118	0,01692	0,0293	0,0968	0,1958	0,2472	0,1944	0,0933	0,0287
Значения (f)	0,0008	0,0054	0,013	0,026	0,037	0,039	0,031	0,0178	0,0077
Dx=	50	16	0	28	22	0	26	16	45
Высота столбца (h)	0,002222	0,001111	0	0,007778	0,024444	0,036667	0,028889	0,004444	0,005556
Число попаданий (mi)	2	1	0	7	22	33	26	4	5
Сложение чисел попаданий	2	3	3	10	32	65	91	95	100
Сложение частот (Σmi)	0,02	0,03	0,03	0,1	0,32	0,65	0,91	0,95	1
χ2	7,056344	6,467414	3,216689	0,556033	0,127497	0,066278	0,106667	0,048114	1,218432

	Таблица №2 Расчётные данные частоты, вероятности, значения функции и χ2

 

mx*=	995,5
Dx*=	178
σ =	13,5

	Гистограмма №1 закон распределение

Таблица №3 Расчётные значения mx*, Dx*, σ,

Гистограмма №2 Накопленный полигон(1) и кумулятивная  кривая (2)

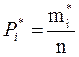, n – число измерений(100);  - число попаданий в интервал

Математическое ожидание:

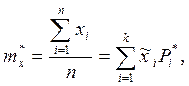
где  - среднее значение случайной величины в i–м интервале;

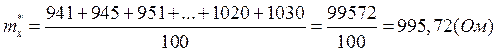
Дисперсия:

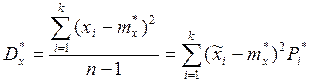
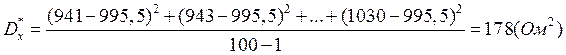
Среднеквадратичное отклонение:

,

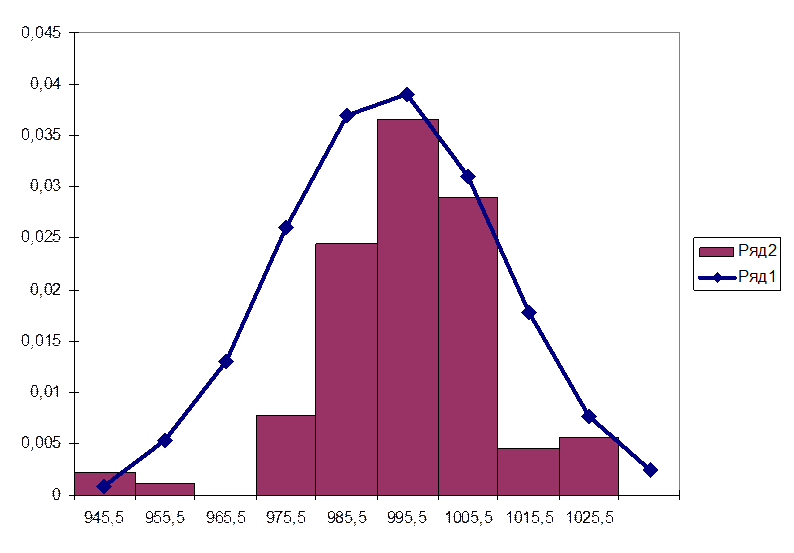
В случае нормального закона плотность распределения f(x) вi–й точке будет 

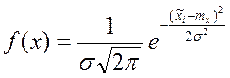
полученные данные занесены в таблицу №2

Нахождение вероятности ( ):

,

где .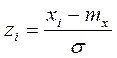

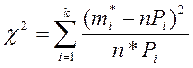
- мера отклонения.

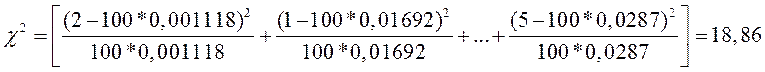
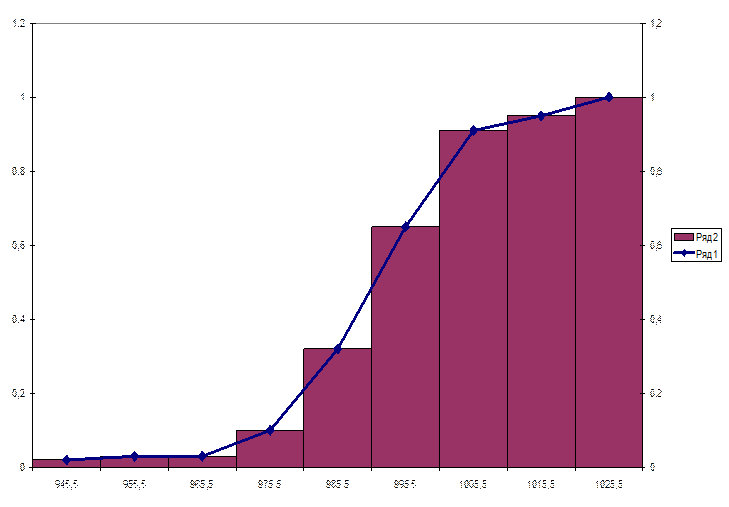
Метод вероятностных сеток.

L=120 мм; ∆х=89 Ом;

K_R=120/89=1,3 мм/Ом;

S(x)=x	945,5	955,5	965,5	975,5	985,5	995,5	1005,5	1015,5	1025,5
F(x)	0,02	0,03	0,03	0,1	0,32	0,65	0,91	0,95	1
SF	-99,6	-91,2	-91,2	-62,2	-22,7	20	65	79,8	150

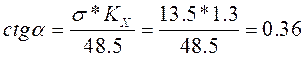
α=64°; m_R=989,9 мм;

σ_R=18,7 мм

χ²=18.9

Величину критерия Пирсона нельзя назвать малой и не все точки лежат на проведенной прямой, поэтому гипотезу о нормальном законе распределения нельзя принять.

Вывод. В ходе выполнения работы было получено 100 значений дискретной случайной величины – сопротивления резисторов. Была выдвинута гипотеза о нормальном законе распределения этой случайной величины. Гипотеза проверялась методом моментов и методом вероятностных сеток. В результате проверки гипотезы методом моментов была построена теоретическая кривая плотности нормального закона распределения, которая оказалась несогласованной со статистическими данными по оценке критерия Пирсона. В результате проверки гипотезы методом вероятностных сеток был построен прямолинейный график функции нормального распределения на вероятностной сетке, который также не согласуется со статистическими данными по методу наименьших квадратов и по оценке критерия Пирсона. Т.о. гипотезу о нормальном законе распределения дискретной случайной величины принять нельзя.

Вывод:_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________