Какими частотными и фазовыми характеристиками должен обладать этот импульс для обеспечения заданной задержки импульса без искажений

Выясним какими частотными и фазовыми характеристиками должен обладать этот импульс для обеспечения заданной задержки импульса без искажений.

Положим, что выходной импульс снимается в виде напряжения. В этом случае следует рассматривать частотную и фазовую характеристику коэффициента передачи.

Поскольку коэффициент передачи определяет и изменения амплитуды импульса и искажение его формы (фронтов и вершин), то идеальная не искажающая система должна иметь коэффициент передачи не зависящей от , и

.

Модуль его не должен зависеть от

.

Фаза коэффициента передачи

, должны меняться по линейному закону.

Действительно если на вход системы подано напряжение которое можно записать в виде интеграла Фурье,

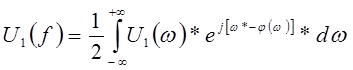, то учитывая (1) и (2) получим

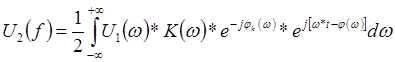
или

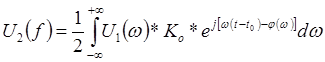, то есть  и  отличаются постоянным множителем  и мементом начала отсчета времени.

Следовательно: импульс на выходе системы не отличается по форме от импульса на входе системы, но задерживается системой на время 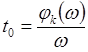, равное крутизне фаза – частотной характеристики.

Для иллюстрации этого факта рассмотрим прохождение через ИП гармонического колебания.

Пусть .

Тогда, если , то колебания на выходе отстают по фазе от колебаний на входе на величину , то есть

.

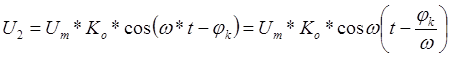Этому сдвигу фаз соответствует смещение максимумов колебаний на величину .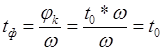

Поэтому очевидно, что все гармонические колебания составляющие импульса появляются на выходе идеальной линии задержки в том же соотношении фаз, что и на входе.

А поскольку , амплитуды всех гармонических составляющих импульса находятся в прежнем состоянии.

Поэтому форма импульса на выходе соответствует форме импульса на входе.

Реальные системы по частотным характеристикам  отличаются от рассмотренной идеальной системы, так как в реальных системах коэффициент передачи может зависеть от частоты, что приводит к нарушению соотношения амплитуд и фаз отдельных гармонических составляющих задерживаемого импульса.

Поэтому в реальных системах происходит искажение формы импульса, заключающиеся в увеличении длительности фронтов, длительности импульса (по основанию) и искажение плоскости вершины. Импульс становятся расплывчатым.

Эти искажения определяются ограниченностью полосы пропускания реальных систем.

Рассмотрим влияние полосы пропускания на форму производимого импульса.

Для упрощения анализа будем считать, что , то есть фазовые искажения отсутствуют, а коэффициент передачи за пределами полосы пропускания равен 0.

При этом внутри полосы пропускания , то есть при .

Пусть на вход системы поступают импульсы 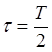, напряжение такой формы можно представить рядом Фурье.

, .

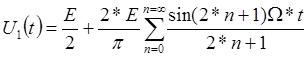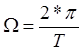Этому ряду соответствует изображение …

В результате ??? полосы пропускания на выходе ИП  будут содержаться только гармонические составляющие ??? .

Причем для каждой из этих составляющих спектра можно записать:

.

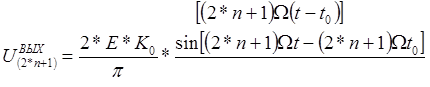Таким образом постоянная составляющая на входе системы будет равна 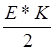, а все составляющие с  будут отсутствовать, так как величина  для этих частот.

Таким образом напряжение на выходе системы определяется .

.

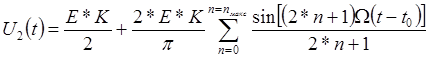Иначе определяется и находится из условия

.

Следовательно выходное напряжение отличается от входного как сдвигом начала отсчёта, и составом спектра.

Посмотрим, как передается через такую систему фронт импульса.

Для определения линейной скорости нарастания импульса продифференцируем (2).

.

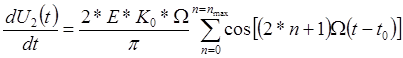Отсюда видно, что при , каждый член этой суммы достигает максимального значения (равного 1), а число составляющих спектра равно .

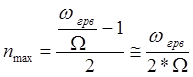, и при  скорость нарастания напряжения максимальна.

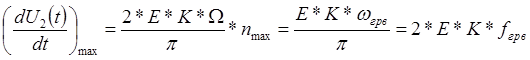
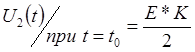 и через определенный промежуток времени устанавливается напряжение , то есть при воздействии скачка на входе импульс будет иметь вид …

Для комплексной оценки длительности нарастания напряжения на выходе выполним следующее построение:

в точке 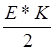 (А) проведём касательную и будем рассматривать её часть заключенную между осью времени м уровнем , как приближенное изображение фронта нарастания напряжения.

Средняя часть нарастания  отстает на время запаздывания , равное крутизне частотной характеристики. Скорость нарастания, как мы приняли равна:

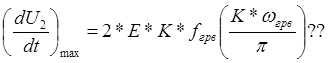(и растет с расширением полосы пропускания).

Как видно из рисунка 9^(а) продолжительность нарастания определяется из прямоугольного треугольника BCD катетами которого являются величины  и искомая величина , а также угла наклона гипотенузы .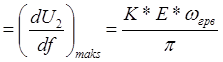

Отсюда 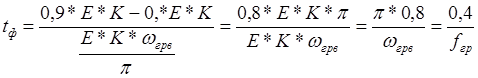, так как  отсчитывается между уровнями 0б1 и 0б9 от максимального.

Этот результат позволяет приближенно определить длительность процесса установления в системах с фаза – частотной характеристикой, близкой к идеальной. Поэтому для определения близости нарастания необходимо знать .

Линии задержки с равномерно распределенными параметрами.

Линии задержки с равномерно распределенными параметрами представляют собой отрезок однородной неискажающей линией длиной R, нагруженной на активное сопротивление, равное волному сопротивлению линии, то есть,

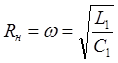 (L₁ – C₁ – погонные параметры).

Как видно из определения подобная линия представляет собой идеальное устройство временной задержки. Такая линия работает в режиме бегущей волны.

Как мы рассматривали ранее, для такого идеального устройства , где: 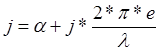 - постоянная распространения.  - коэффициент затухания линии;  - длина волны распространяющейся вдоль линии колебаний с частотой - .

Как мы выяснили для идеальных ИП

.

Функцию   в данном случае можно представить так:

.

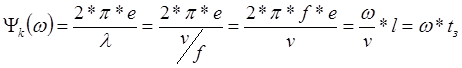Скорость распространения волн вдоль линии (фазовая скорость) 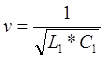 и временная задержка сигнала в однородной длинной линии будет равна времени распространения волны вдоль линии: .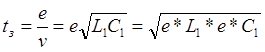

Таким образом длинные линии могут быть использованы в качестве линий задержки, обладающих идеальными параметрами в  полосе частот

Конструктивно они выполняются в виде отрезков высококачественных экранированных кабелей типа РК= волновым сопротивлением 50 – 100 Ом.

Такие линии задержки позволяют получить практически неискаженный задержанный сигнал и применяются для задержек импульсов на мили – микро секунды.

Что бы получить задержку импульса на 1 мкс необходим кабель около 200 метров длины.

Поэтому использование линии задержки с большим временем задержки связано со значительными конструктивными трудностями, и неприменимо в малогабаритной аппаратуре.

Вернуться к содержанию