Определение диаметра трубы сифона при условии работы только одного из сифонов. Проверка режима движения и области сопротивления

Санкт-Петербургский государственный политехнический университет

Инженерно-строительный факультет

Кафедра гидравлики

Расчетно-графическая работа № 2 по курсу гидравлики

«Расчет коротких трубопроводов»

(тип 3)

Выполнила:   Беллендир Н.Э.

группа 3013/1

Проверила:   Локтионова Е.А.

Санкт-Петербург

2011г

Оглавление

1      Определение диаметра трубы сифона при условии работы только одного из сифонов. 3

2      Проверка режима движения и области сопротивления. 9

3      Построение напорной и пьезометрической линий в предположении, что работает один сифон. 11

4      Проверка максимального вакуума в сифоне. 13

5      Нахождение разности уровней в водоемах A и B в предположении, что работают оба сифона. 14

Литература. 15

1  Определение диаметра трубы сифона при условии работы только одного из сифонов

Запишем общий вид уравнения Бернулли:

,

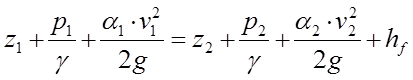где ,  - превышения над плоскостью сравнения, м; ,  - гидродинамические давления, Па;  - удельный вес жидкости, Н/м³; ,   - коэффициенты кинетической энергии; ,  - средние скорости в сечениях, м/с; - полная потеря напора, м; - ускорение свободного падения, м/с².

В данном случае нам необходимо решить задачу на расчет короткого трубопровода (рис.1), для этого воспользуемся формулой расхода, которую можно получить из уравнения Бернулли:

                                                   (1.1)

где  - расход жидкости в трубе,  м³/с;  - коэффициент расхода;  - площадь поперечного сечения трубы, м².

В этой формуле 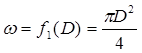 и , в связи с чем найти непосредственно диаметр D уравнения (1.1) нельзя. Поэтому это уравнение приходится решать подбором.

С этой целью преобразуем выражение (1.1):

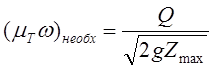,                                     (1.2)

где - расчетный расход обоих сифонов, м³/с (=0,07 м³/с); - наибольшее превышение оси трубы сифона над уровнем воды в водоеме А, м (= 4,2 м).

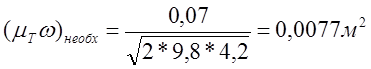
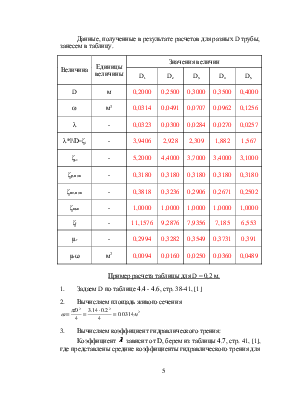
Данные, полученные в результате расчетов для разных D трубы, занесем в таблицу.

Величина	Единицы величины	Значения величин
		D1	D2	D3	D4	D5
D	м	0,2000	0,2500	0,3000	0,3500	0,4000
ω	м2	0,0314	0,0491	0,0707	0,0962	0,1256
λ	-	0,0323	0,0300	0,0284	0,0270	0,0257
λ*l\D=ζl	-	3,9406	2,928	2,309	1,882	1,567
ζвх	-	5,2000	4,4000	3,7000	3,4000	3,1000
ζр.пов	-	0,3180	0,3180	0,3180	0,3180	0,3180
ζпл.пов	-	0,3818	0,3236	0,2906	0,2671	0,2502
ζвых	-	1,0000	1,0000	1,0000	1,0000	1,0000
ζf	-	11,1576	9,2876	7,9356	7,185	6,553
μт	-	0,2994	0,3282	0,3549	0,3731	0,391
μтω	м2	0,0094	0,0160	0,0250	0,0360	0,0489

Пример расчета таблицы для D = 0,2 м.

1.  Задаем D по таблице 4.4 - 4.6, стр. 38-41, [1]

2.  Вычисляем площадь живого сечения

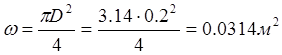
3.  Вычисляем коэффициент гидравлического трения:

Коэффициент  зависит от D, берем из таблицы 4.7, стр. 41, [1], где представлены средние коэффициенты гидравлического трения для бывших в эксплуатации чугунных труб при D = (1,0 - 1,5) мм (квадратичная область сопротивления).

Для бывших в эксплуатации труб с D = 0,2 м  λ_ср = 0,0323.

4.  Найдем коэффициент сопротивления по длине, воспользовавшись формулой:

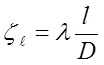,                                                   (1.3)

где l - длина трубы сифона, м (l = 4*(Zmax + h`) = 4*(3,6 + 2,5) = 24,4 м);  - коэффициент гидравлического трения; D - диаметр поперечного сечения трубы, м.

 

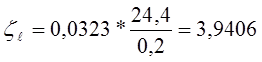
5.  Найдем коэффициент сопротивления входа:

В данной задаче ζ_вх = ζ_кл.

Коэффициент сопротивления всасывающего клапана с сеткой, который зависит от D, берем из табл. 4.16, стр. 50 [1].

Для труб с D = 0,2 м ζ_кл = 5,2.

6.  Найдем коэффициент сопротивления резкого поворота:

В данной задаче имеется 2 резких поворота θ₁ = θ₃ = 45  (рис. 1).

Коэффициент сопротивления резкого поворота берем из таблицы 4.18, стр.51, [1].

Для α  = 45  ζ_р.пов = 0,318

7.  Найдем коэффициент сопротивления плавного поворота для трубы круглого поперечного сечения находим по формуле:

,                                            (1.4)

где  - коэффициент, зависящий от угла поворота и определяемый по опытным данным Кригера (таблица 4.20, стр.52, [1]);  - коэффициент сопротивления при угле поворота 90 , определяемый по таблице 4.21, стр. 53, [1] или по формуле:

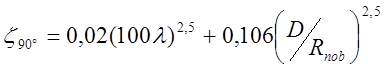                         (1.5)

В данной задаче имеется 1 плавный поворот θ₂ = 90 . Следовательно, = 1.

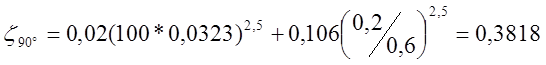
8.  Примем ζ_вых = 1 .

9.  Найдем полный коэффициент сопротивления по формуле:

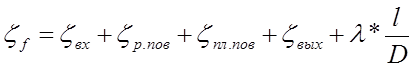                   (1.6)

10.  Вычисляем коэффициент расхода трубопровода по формуле:

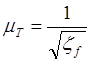                                                      (1.7)

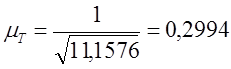
11.  Рассчитаем  :

По данным таблицы на рис.2 строится график зависимости D от . Для нахождения искомого диаметра трубы сифона из графика  находится значение D, соответствующее значению , и округляется до большего стандартного значения.

D_иск = 0,2 м.

Далее необходимо провести проверку правильности расчета по формуле:

,                                                   (1.8)

где  - действительное значение разности уровней в водоемах, м, определяемое по формуле:

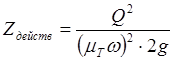                                          (1.9)

Единственное значение μ_тω при котором  больше нуля = 0,0094

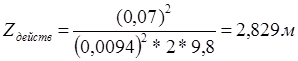
Проверка прошла успешно, следовательно, расчеты были проведены  верно.

2  Проверка режима движения и области сопротивления

Для проверки режима движения в трубе необходимо вычислить число Рейнольдса и сравнить его с известными критическими значениями, если:

·   - ламинарный режим движения;

·   - турбулентный режим движения.

Скорость υ считаем по формуле:

 

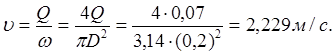
Число Рейнольдса Re_D вычисляется по формуле:

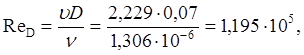
где - коэффициент гидравлического трения, м²/с (задаем по таблице 2.12, стр. 16, [1]; для воды при t = 10°C = 1.306*10^-6).

.

Следовательно, в данной трубе турбулентный режим движения.

3  Построение напорной и пьезометрической линий в предположении, что работает один сифон

Для построения пьезометрической и напорной линии нам необходимо знать величины потерь напора по длине на каждом участке, местных потерь напора, а также величину скоростного напора.

Потери напора по длине

Считаем по формуле:

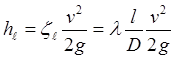.                                       (3.1)

Для выбранного нами диаметра D = 0,2 м значение коэффициента гидравлического трения l = 0,0323, скорость воды v = 2,229 м/с, а l берется из исходных данных длин участков, и считаем по формуле (3.1) значения потерь напора по длине на каждом участке:

·  Первый и четвертый участок (l₁ = l₄ = 2,44 м):

.

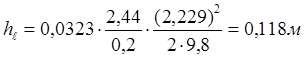·  Второй и третий участок (l₂  = l₃ = 9,76 м):

.

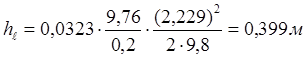Местные потери напора.

Считаем по формуле:

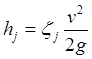.                                                    (3.2)

·  Коэффициент сопротивления всасывающего клапана с сеткой , тогда по формуле (3.2):

 .

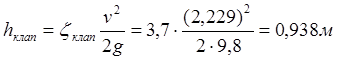·  Резкий поворот на 45° (первый и третий):

.

Тогда по формуле (3.2):

 .

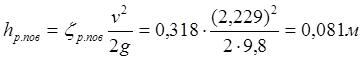·  Если плавный поворот на 90°, то = 0,3818.

По формуле (3.2) получаем:

 .

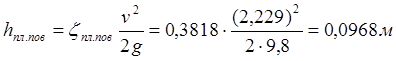·  Для выхода было принято значение = 1.

По формуле (2.2) получаем:

 .

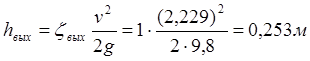·  Сложим получившиеся значения потерь напора:

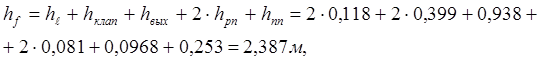
т. е. примерно равно найденной нами ранее разности уровней в водоемах А и В Z_действ.

На рис. 1 построим напорную линию Е-Е, для этого откладываем в масштабе значения потерь напора, начиная с горизонта жидкости в питающем водоеме A и заканчивая на уровне воды в нижнем бьефе.

Пьезометрическая линия Р-Р всюду отстоит от напорной на постоянную величину скоростного напора, которую вычислим по формуле:

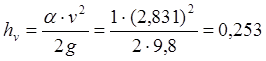 м,

где a - корректив кинетической энергии (принимаем a = 1).

4  Проверка максимального вакуума в сифоне

Сразу за поворотом в самом верхнем сечении трубы образуется максимальный вакуум.

Используя метод графической интерполяции, проверим не превышает ли максимальный вакуум в данной задаче допускаемый вакуум:

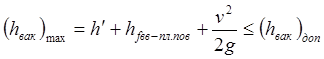,                        (4.1)

где  - допускаемый вакуум по условию неразрывности сплошной струи.

Для воды при нормальных условиях берем значение  = 7 м вод. ст.

  

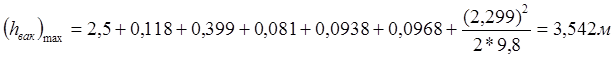
Проверка максимального вакуума в сифоне выполнена.

5  Нахождение разности уровней в водоемах A и B в предположении, что работают оба сифона

Для нахождения нового значения разности уровней в водоемах воспользуемся формулой 1.9.

Поскольку теперь работают оба сифона, то расход воды, проходящий через один сифон, уменьшится в два раза (Q` = Q/2).

 .

Литература

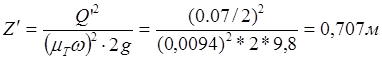1. Механика жидкости и газа (гидравлика): Учебник для вузов / Гиргидов А.Д. СПб.: Изд-во СПбГПУ, 2002. 546 с.

2. Механика жидкости и газа (гидравлика): Метод. рекомендации для выполнения и оформления курсовых и расчетно-графических работ / Е.Н. Кожевникова, Е.А. Локтионова, В.Т. Орлов. СПб.:Изд-во СПбГПУ,2006. 39 с.

3. Механика жидкости и газа (гидравлика). Краткий справочник: Учеб. пособие / Е.Н. Кожевникова, А.И. Лаксберг, Е.А. Локтионова. СПб.: Изд-во СПбГПУ, 2003. 72 с.