Спектры колебаний в электронных устройствах, страница 4

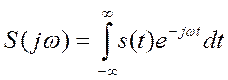
Восстановить колебание по известному спектру можно с помощью формулы обратного преобразования Фурье.

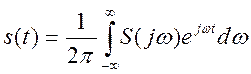
Эти два выражения позволяют для непериодических сигналов выполнять все преобразования, которые возможны для периодических колебаний с помощью рядов Фурье. Периодические колебания  являются математической абстракцией, так как предполагается, что они существуют на бесконечном интервале времени. Непериодические колебания ближе к реальным сигналам, поэтому преобразование Фурье, основанное на спектральной плотности, является общим случаем,  в практике спектрального анализа применяется чаще и в теории сигналов считается основным.

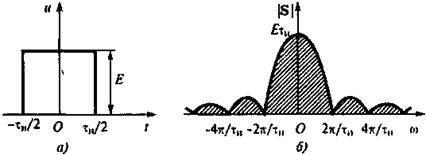
Рис.2.5

На рис. 2.5 для примера приведена временная диаграмма и спектральная плотность одиночного прямоугольного импульса. Импульс соответствует последовательности импульсов, представленной на рис. 2.3 и 2.4.  По форме спектр одиночного импульса совпадает с огибающей спектра периодической последовательности. Для наглядности отображения сплошного спектра на рис.2.5 пространство под кривой спектральной плотности заштриховано. Обычно штриховка не выполняется.

2.3. Примеры спектров колебаний

В таблице 2.1 приведены спектры колебаний наиболее распространенных в электронных устройствах.

Таблица 2.1

Сигнал	Спектральная плотность

Из приведенных спектров видно, что дельта-функция обладает наиболее широким спектром. Эта функция является математической абстракцией, так как под ней понимается бесконечно короткий импульс с бесконечно большой амплитудой и единичной площадью импульса. Реальным аналогом дельта-функции является просто очень короткий импульс, ширина спектра которого значительно больше полосы пропускания анализируемого электронного устройства.

Сравнивая спектр дельта-функции со спектром прямоугольного импульса можно заметить, что ширина последнего уменьшается с увеличением длительности. Амплитуда низкочастотных составляющих спектра с увеличением длительности увеличивается за счет быстрого уменьшения амплитуд высокочастотных составляющих. Это означает, что чем медленнее меняется сигнал, тем уже его спектр.  

Если длительность импульсов фиксировать и менять только форму импульсов, то увидим, что ширина спектра зависит от наличия на временной диаграмме сигнала участков с резкими изменениями. Такие изменения отсутствуют в импульсах колоколообразной формы. Плавная форма этих импульсов приводит к тому, что спектр у них самый узкий.

2.4. Свойства преобразований Фурье

А) Преобразование Фурье является линейным, т. е. спектр суммы колебаний равен сумме спектров этих колебаний:

  
           Б) Увеличение амплитуды колебания s(t) в а раз приводит к увеличению в а раз амплитуд составляющих спектра:

В) Увеличение масштаба времени колебания в а раз приводит к уменьшению в а раз амплитуд составляющих спектра и ширины частотной полосы спектра:

Это очень важное свойство для передачи сигналов по каналам связи, так как показывает, что, например, широкополосные сигналы можно передавать по узкополосным каналам, растянув сигналы во времени (путем записи, к примеру, на магнитную ленту и воспроизведения с пониженной скоростью движения ленты).

Г) Задержка колебания на эквивалентна умножению его спектра на множитель e:

.

Д) Дифференцирование колебания эквивалентно умножении его спектра на :

Е) Интегрирование колебания эквивалентно делению его спектра на :

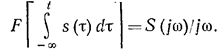3. Описание лабораторного стенда

Экспериментальная часть лабораторной работы выполняется методом моделирования с помощью прикладного пакета Electronic Workbench на персональном компьютере линии IBM PC с производительностью не ниже P150 и оперативной памятью 32 МБ и выше. Рабочее окно пакета приведено ниже.

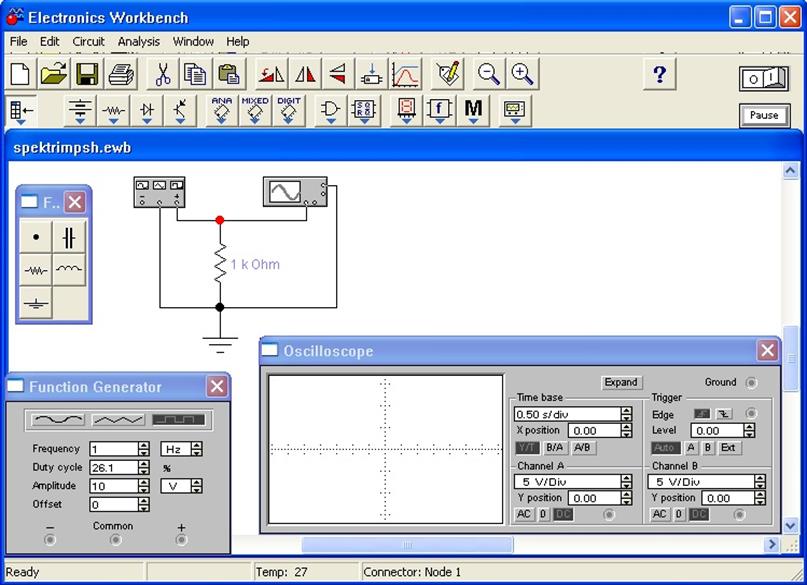
Рис. 3.1

Вызов рабочих панелей генератора и осциллографа можно выполнить двойным щелчком по обозначению прибора на схеме.

3.1. Задание вида генерируемых колебаний производят с помощью кнопок в верхней части панели управления генератора. Возможна генерация одного из трех видов колебаний: гармонические колебания напряжения, импульсы пилообразной формы с линейно изменяющимся напряжением фронтов и прямоугольные импульсы с идеальными прямоугольными фронтами. Задание частоты и амплитуды колебаний производится в полях Frequency и Amplitude. Порядок задания стандартный и пояснений не требуется.