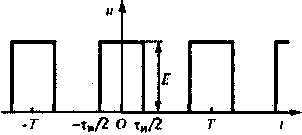Спектры колебаний в электронных устройствах, страница 3

 

Рис. 2.3

Кроме перечисленных параметров импульсы часто характеризуются скважностью

.

Одиночный идеальный прямоугольный импульс описывается уравнением:

т. е. он формируется как разность двух единичных функций s(t)) (функций включения, или функций Хевисайда ), сдвинутых во времени на t_и.

Последовательность прямоугольных импульсов представляет собой известную сумму одиночных импульсов:

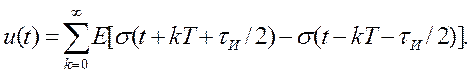
Используя ряд Фурье, получим выражение для комплексных амплитуд составляющих спектра.

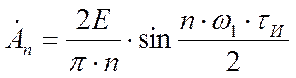
Здесь 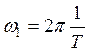 - циклическая частота первой гармоники.

Это выражение показывает, что спектр последовательности импульсов симметричной относительно оси t=0 не содержит мнимых частей в комплексных амплитудах. Амплитуды спектральных составляющих вещественные величины, но знакопеременные.

Амплитудный спектр найдем как модуль комплексного спектра.

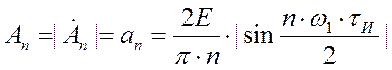
Фазовый спектр найдем как аргумент комплексной амплитуды. Для каждого значения n фаза определяется как аргумент тангенса отношения мнимой части  к действительной. В данном случае мнимая часть равна нулю.

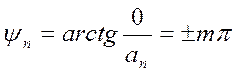
где m=0,1,2,… .

Амплитудный (а) и фазовый (б) спектры последовательности прямоугольных импульсов изображены на рис. 2.4.

Рис.2.4

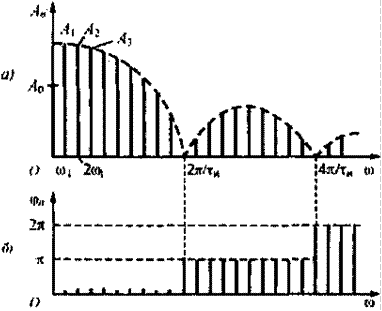Найденный амплитудный спектр заданного сигнала в значительной степени зависит от  величин периода повторения Т и длительности импульса t_И. Очень важно отметить, что при одной и той же длительности импульса t_И с увеличением периода их повторения T основная частота w₁ = 2p/T уменьшается, и линии спектра располагаются плотнее. Если укорачивается длительность импульса t_И при неизменном периоде T,  величина w₁ не меняется и каждая вертикальная линия, обозначающая спектральную составляющую, остается на том же месте оси частот. Меняются высоты линий так, как нули огибающей смещаются по графику вправо, т.е. их частоты увеличиваются.

При изменении величины импульсов амплитуды всех гармоник меняются синхронно. Форма амплитудного спектра при изменении  не меняется.

Линия на графике амплитудного спектра, соответствующая значениям , называется огибающей спектра. Она проходит через вершины линий гармонических составляющих кроме нулевой составляющей, которая имеет вдвое меньшее значение, чем ее коэффициент.

В практике проектирования электронных устройств весьма важной характеристикой сигналов является наивысшая частота составляющих, которые необходимо передать без искажений, превышающих допустимый предел. Для оценки этой частоты пользуются понятием ширины спектра. Под ней понимают область частот, в которой сосредоточена основная часть энергии сигнала. Так как точная оценка искажений достаточно сложна, применяются упрощенные критерии. Наиболее часто употребляется критерий по уровню  (~0,707). При этом верхней и нижней границами ширины спектра(и ) считаются максимальная и минимальная частоты, на которых амплитуды спектральных составляющих равны максимальному значению огибающей () деленной на корень из двух, т.е.

.

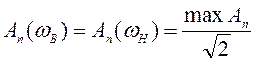Этот критерий подходит для большинства задач передачи и обработки сигналов. Если требования к правильности передачи сигнала повышенные, применяют более жесткий критерий по уровню 0,1.

2.2. Спектры непериодических колебаний

Спектр непериодического колебания не может быть представлен рядом Фурье в приведенном выше виде. Чтобы воспользоваться им, можно искусственно представить непериодическое колебание в виде предела, к которому стремится периодическое колебание при увеличении его периода до бесконечности. При увеличении периода линии спектра начинают сближаться. В пределе спектр становится сплошным и изображается не вертикальными линиями амплитуд спектральных составляющих, а одной кривой проходящей по вершинам линий.

По мере увеличения периода амплитуды составляющих спектра уменьшаются  и в пределе становятся бесконечно малыми величинами. После предельного перехода суммирование в формуле ряда превращается в интеграл. Восстановить исходное колебание по такому ряду математически несложно, но изобразить амплитуды на графике не удастся. По этой причине в качестве спектра непериодического колебания используют  спектральную плотность, определяемую как предел отношения амплитуды спектральной составляющей к разности частот смежных гармоник. Спектральная плотность может быть определена по форме колебания с помощью математического выражения, называемой формулой прямого преобразования Фурье.