Спектры колебаний в электронных устройствах, страница 2

Определение параметров гармоник спектра произвольного колебания выполняется на основе ряда Фурье. В электрических цепях применяется ряд Фурье в комплексной форме, получаемый применением формулы Эйлера к мгновенным значениям спектральных составляющих.

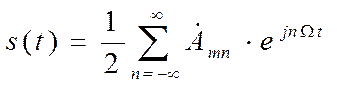                                 (1)

Здесь

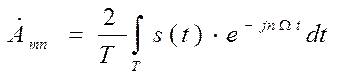                               (2)

- комплексная амплитуда n-й гармоники;

n  – целое число, меняющееся от минус до плюс бесконечности.

Этот ряд имеет компактную и логичную форму записи, но каждая гармоника реального  спектра представлена в нем в виде двух комплексных гармоник с  сопряженными номерами n и -n. Сопряженные гармоники имеют одинаковую амплитуду равную половине амплитуды реальной гармоники. Частоты этих гармоник одинаковы по величине, но частота второй считается отрицательной. Мгновенные значения комплексных гармоник имеют вещественную и мнимую части. Вещественные части обеих комплексных гармоник имеют одинаковые знаки. При суммировании они складываются. Мнимые имеют противоположные знаки, обусловленные отрицательной частотой второй комплексной гармоники, и при суммировании по формуле (1) взаимно компенсируются.

Формула (2) позволяет рассчитать спектр колебания сложной формы, если известно само колебание. Преобразование колебания в спектр называют прямым преобразованием Фурье.  Формула (1) решает обратную математическую задачу, т.е.  позволяет рассчитать само колебание по известному спектру. Это действие называют обратным преобразованием Фурье.

Амплитудный спектр является четной функцией. Получить его можно, если учесть что комплексная амплитуда содержит обычную амплитуду n – й составляющей спектра A_mn и ее фазу .

Для построения графика амплитудного спектра достаточно определить модуль комплексной амплитуды.

Пример возможного графика амплитудного спектра для комплексной формы ряда Фурье приведен на рис. 2.2. Здесь он построен с учетом множителя ½ в формуле (1).

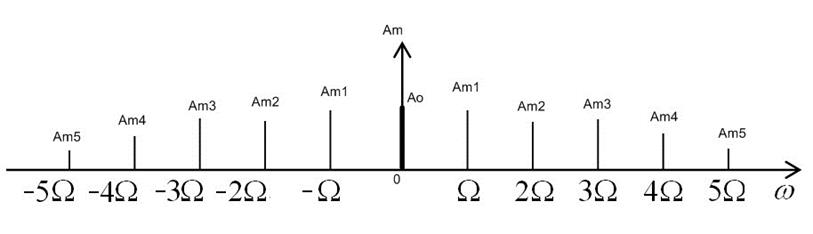
Рис. 2.2

При графическом представлении спектров нерационально рисовать обе половины спектра, поэтому изображают только правую. Такой график соответствует реальным амплитудам спектра. Именно эту форму спектра выводит на экран моделирующая программа пакета Workbench. Спектральные преобразования в этом случае описывается следующими выражениями.

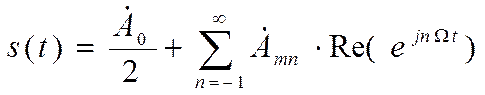,                          (3)

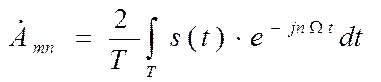.                        (4)

Здесь  -  реальная часть экспоненты с комплексной степенью.

2.1.3. Определение ширины спектра.

Весьма важной частотной характеристикой колебания является ширина его спектра, под которой понимаются верхняя и нижняя частотные границы, в пределах которых амплитуды спектральных составляющих должны воспроизводиться с достаточной точностью. За пределами ширины спектра точность воспроизведения амплитуд не нормируется и допускается ее уменьшение. Очевидно, что число правильно воспроизводимых гармоник должно рассчитываться исходя из необходимой точности восстановления колебания по его спектру. Однако практически для приближенной оценки ширины часто используют упрощенные критерии. Наиболее часто применяют критерий, при котором в ширину спектра включают все составляющие с величиной мощности большей, чем половина мощности гармоники с максимальным значением A_mn. Так как спектр изображается в виде амплитуд, пересчитывать их в мощности достаточно неудобно. По этой причине обычно пользуются тем, что мощность пропорциональна амплитуде во второй степени. В качестве границ используют максимальное значение A_mn, деленное на корень из двух.

Правильная передача постоянной составляющей спектре колебания или близких к ней частот нередко имеет принципиальное значение. В этом случае в качестве нижней границы используют нулевое значение и ширину спектра определяют только по верхней границе.

При желании получить большую точность представления колебания с помощью спектра иногда используют критерий 0,1 от максимального значения A_mn. Спектр получается при этом шире, а точность представления значительно выше.   Примеры определения ширины спектра приведены при рассмотрении спектра прямоугольных импульсов.

2.1.4. Спектр периодической последовательности прямоугольных импульсов

Рассчитаем амплитудный и фазовый спектры периодической последовательности прямоугольных видеоимпульсов, имеющих амплитуду Е, длительность t_и, период повторения Т и расположенных симметрично относительно начала координат  (рис. 2.3).