Проверка гипотезы о нормальном законе распределения параметра радиоэлемента

Федеральное агентство по образованию РФ

Государственное образовательное учреждение высшего профессионального образования

"Владимирский государственный университет"

Кафедра КТРЭС

Лабораторная работа № 1

Проверка гипотезы о нормальном законе распределения параметра радиоэлемента

Вариант № 16

Выполнил: ст.гр. Р-107

Проверил:

Владимир, 2010

Цель работы: Проверка  гипотезы  о  нормальном  законе  распределения статистических  данных на трех различных линиях.

Исходные данные.

ряд 1: 499,505,522,481,512,494,466,489,497,515,464,515,501,532,505,496,452,505,512,493,490,506,496,482,496,500,489,515,505,494,527,503,510,506,484,532,486,499,506,465,519,530,495,498,480,515,519,516,473,487.

ряд 2: 507,511,528,491,505,500,504,500,529,530,528,541,498,512,557,525,531,563,539,546,546,542,509,516,546,543,546,572,550,575,537,597,571,578,569,583,567,611,574,581,559,578,603,608,562,583,575,587,602,593.

ряд 3: 607,630,556,603,616,576,573,604,585,573,575,582,609,587,574,586,612,566,562,553,549,546,564,567,560,554,523,512,538,534,530,532,545,570,542,526,507,560,524,512,497,513,528,533,495,499,505,483,518,469.

Ход работы.

Ряд 1

Контрольный лист для 1-го ряда представлен в таблице 1.

Таблица 1 – Контрольный лист для 1-го ряда

Высота прямоугольника  гистограммы  находится  по  формуле

.

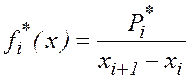Среднее  арифметическое  значение  параметра  рассчитывается  по формуле

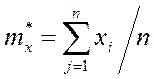
или  приближенно  по  формуле

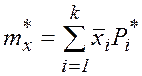 , где  k– число  разрядов, - середина  i-го  интервала.

Статистическая  дисперсия

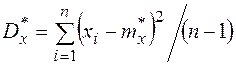
или  приближенно

.

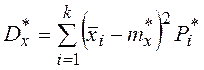Некоторые промежуточные результаты расчетов сведены в таблицу 2.

Таблица 2 – Промежуточные результаты обработки данных

Интервал		Середина интервала,	Частота, mi	Относительная частота,	Накопленная частота,	Относительная накопленная частота,
от	до
439	452	445,5	5	0,1	5	0,1
452	465	458,5	1	0,02	6	0,12
465	478	471,5	2	0,04	8	0,16
478	491	484,5	3	0,06	11	0,22
491	504	497,5	4	0,08	15	0,3
504	517	510,5	8	0,16	23	0,46
517	530	523,5	5	0,1	28	0,56
530	543	536,5	10	0,2	38	0,76
543	556	549,5	10	0,2	48	0,96
556	569	562,5	2	0,04	50	1

По таблице 2 строятся гистограмма и кумулятивная кривая (рис. 1, 2).

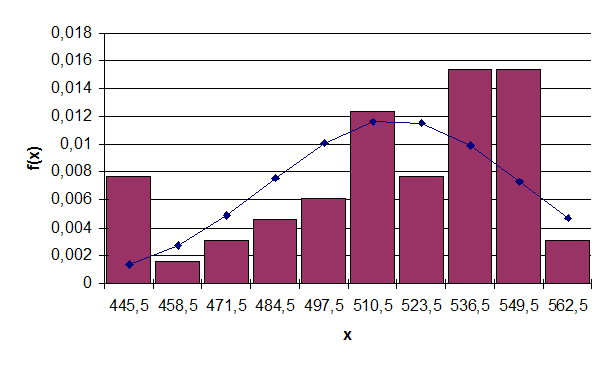
Рис. 1. Гистограмма для 1-го ряда

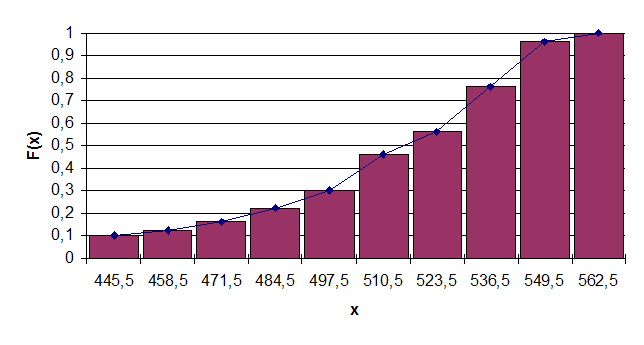
Рис. 2. Кумулятивная кривая для 1-го ряда

При четном числе измерений медиана представляет собой среднее арифметическое двух значений, расположенных в середине ряда

.

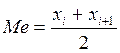Для первого ряда получается

.

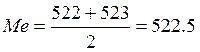Модой называется наиболее часто встречающееся значение случайной величины в ряду. Для первого ряда мода равна 539.

Гипотеза о нормальном законе распределения проверяется с помощью критерия Пирсона, который рассчитывается по формуле