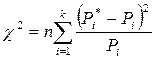Проверка гипотезы о нормальном законе распределения параметра радиоэлемента, страница 2

, где  - относительная частота из таблицы 2, - теоретическая  вероятность  попадания  параметра  x  в  i-й  интервал, которая определяется как

.

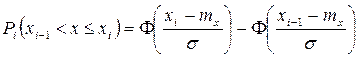Результаты расчета критерия Пирсона сведены в таблицу 3.

Таблица 3 – Расчет критерия -Пирсона

Граница интервала			Вероятность попадания в интервал
439	-2,28968	0,0113	0,0168	-	0,412038	-
452	-1,90561	0,0281		0,0362		0,00725
465	-1,52153	0,0643	0,0628		0,008278
478	-1,13746	0,1271		0,0995		0,015681
491	-0,75338	0,2266	0,1403		0,025917
504	-0,3693	0,3669		0,1371		0,003825
517	0,014772	0,504	0,1514		0,01745
530	0,398848	0,6554		0,1269		0,042109
543	0,782925	0,7823	0,0967		0,11035
556	1,167001	0,879		0,0604		0,00689
569	1,551077	0,9394	-		-
					32,48938

Для числа степеней свободы  и уровня значимости р = 0,9 критерий      -Пирсона равен . Видно, что , т.е. гипотезу о нормальном законе распределения принять нельзя.

Числовые характеристики 1-го ряда сведены в таблицу 4.

Таблица 4 – Характеристики 1-го ряда

Ряд 2

Контрольный лист для 2-го ряда представлен в таблице 5. По ней строятся гистограмма и кумулятивная кривая (рис. 3, 4).

Таблица 5 – Контрольный лист для 2-го ряда

В таблице 6 приведены промежуточные результаты расчетов.

Таблица 6 – Промежуточные результаты обработки данных

Интервал		Середина интервала,	Частота, mi	Относительная частота,	Накопленная частота,	Относительная накопленная частота,
от	до
453	465	459	3	0,06	3	0,06
465	477	471	1	0,02	4	0,08
477	489	483	3	0,06	7	0,14
489	501	495	8	0,16	15	0,3
501	513	507	3	0,06	18	0,36
513	525	519	2	0,04	20	0,4
525	537	531	9	0,18	29	0,58
537	549	543	3	0,06	32	0,64
549	561	555	8	0,16	40	0,8
561	573	567	1	0,02	41	0,82
573	585	579	3	0,06	44	0,88
585	597	591	4	0,08	48	0,96
597	609	603	2	0,04	50	1