Проверка гипотезы о нормальном законе распределения параметра радиоэлемента, страница 4

Интервал		Середина интервала,	Частота, mi	Относительная частота,	Накопленная частота,	Относительная накопленная частота,
от	до
446	459,25	452,625	4	0,08	4	0,08
459,25	472,5	465,875	1	0,02	5	0,1
472,5	485,75	479,125	4	0,08	9	0,18
485,75	499	492,375	3	0,06	12	0,24
499	512,25	505,625	5	0,1	17	0,34
512,25	525,5	518,875	5	0,1	22	0,44
525,5	538,75	532,125	5	0,1	27	0,54
538,75	552	545,375	5	0,1	32	0,64
552	565,25	558,625	4	0,08	36	0,72
565,25	578,5	571,875	7	0,14	43	0,86
578,5	591,75	585,125	6	0,12	49	0,98
591,75	605	598,375	1	0,02	50	1

Построенные по таблице 9 гистограмма и кумулятивная кривая изображены на рис. 5, 6.

В таблице 11 представлены результаты расчета критерия Пирсона для 3-го ряда.

В таблице 12 представлены числовые характеристики 3-го ряда.

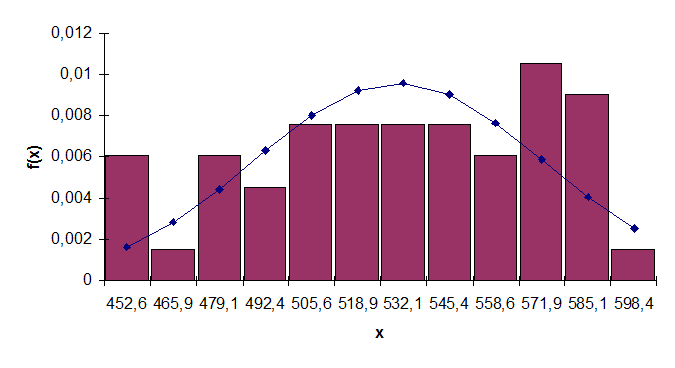
Рис. 5. Гистограмма для 3-го ряда

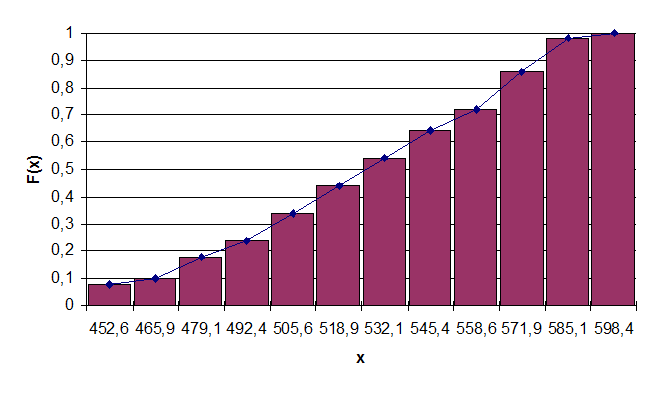
Рис. 6. Кумулятивная кривая для 3-го ряда

Таблица 11 – Расчет критерия -Пирсона

Граница интервала			Вероятность попадания в интервал
446	-2,04037	0,0207	0,022	-	0,1529091	-
459,25	-1,72119	0,0427		0,0381		0,0085987
472,5	-1,402	0,0808	0,0593		0,0072258
485,75	-1,08282	0,1401		0,0835		0,0066138
499	-0,76363	0,2236	0,1064		0,0003850
512,25	-0,44445	0,33		0,1183		0,0028309
525,5	-0,12526	0,4483	0,127		0,0057402
538,75	0,19392	0,5753		0,1197		0,0032422
552	0,513104	0,695	0,1017		0,0046302
565,25	0,832289	0,7967		0,0782		0,0488394
578,5	1,151473	0,8749	0,0543		0,0794934
591,75	1,470657	0,9292		0,0379		0,0084541
605	1,837339	0,9671	-		-
					16,4481274

Для числа степеней свободы  и уровня значимости р = 0,9 критерий      -Пирсона равен . Видно, что , т.е. гипотезу о нормальном законе распределения принять нельзя.

Таблица 12 – Характеристики 3-го ряда

Вывод: В ходе выполнения лабораторной работы было проведено статистическое исследование 3-х выборок, в каждой из которых было по 50 измерений. В ходе анализа для каждого ряда были вычислены следующие числовые характеристики статистических рядов: мода, медиана, среднее арифметическое, статистическая дисперсия и среднеквадратичное отклонение (см. таб. 4, 8, 12). Для всех рядов были составлены контрольные листы (таб. 1, 5, 9) и построены гистограммы и кумулятивные кривые (рис. 1-6). С помощью метода моментов была проверена гипотеза о нормальном законе распределения в каждом из рядов. После вычисления критерия Пирсона и сравнения с тем, что приведен в таблицах для соответствующего числа степеней свободы, выяснилось, что ни для какого ряда нельзя принять гипотезу о Гауссовском законе распределения параметра радиоэлемента.