Использование частичного разнесения сигналов для борьбы с узкополосными и импульсными помехами

Лекция 26. Использование частичного разнесения сигналов для борьбы с узкополосными и импульсными помехами

Классические методы разнесенного приема, такие, как частотное, пространственное или временное разнесение, реализуют кратность разнесения N равную целому числу. В том случае, когда при частотном разнесении сигнала для передачи полезного сигнала используются несколько самостоятельных каналов, тогда кратность разнесения - целое число. Однако бывают ситуации, когда в распоряжении системы связи имеется полоса частот П_К, несколько более широкая, чем полоса сигнала П_C, однако ее избыток недостаточен для организации второго частотно-разнесенного канала. Подобная ситуация позволяет в значительной степени устранять воздействие сосредоточенных и импульсных помех.

Сущность метода обработки сигналов заключается в следующем. На передающей стороне, на основе исходного информационного сигнала x(t) формируется другой сигнал y(t), излучаемый в пространство, , где L{x}-некоторая операция над сигналом x, которая является комбинацией сдвига по частотной оси целиком всего спектра П_С сигнала x(t) на некоторую величину  и, если необходимо, одновременного сдвига по времени на величину . 

Рассмотрим метод в установившемся режиме, первоначально в отсутствии помех и искажений. На вход приемника приходит сигнал . Эти копии разделяются с помощью включенных встречно корреляционных компенсаторов на xL{x}. Далее над копией x производятся операции сдвига по частоте и по времени, в результате чего обе копии полезного сигнала станут совпадать, а узкополосные и импульсные помехи раздвинутся по частоте и по времени и могут быть устранены без повреждения полезного сигнала.

Таким образом, за счет ограниченной избыточности, которую предоставляет канал связи, можно организовать частичное разнесение с тем, чтобы после восстановления двух копий полезного сигнала, по-разному пораженных сосредоточенной или импульсной помехами, исключить воздействии помехи.

Ограничения предложенного метода заключаются в особенностях установления стационарного режима работы схем. Поскольку после компенсаторов копии сигналов x и L{x₂}в некоторой степени могут отличаться от исходных сигналов xи L{x}, то необходимо, чтобы не происходило накопления подобных отличий при многократном прохождении сигналов по петлям обратной связи.

При этом основным препятствием к накоплению отличий служит факт, что при суммировании полезные составляющие складываются синфазно, а отличия, представляющие собой сумму компонент-результатов многократного проведения операции L{x}, взятых с различными весами, складываются произвольным образом, что дает преимущество полезным компонентам. Кроме того, с каждым повторным применением операции , результат каждый раз сдвигается по частотной оси на величину Δf. Таким образом, этот компонент постепенно уходит за полосу тракта, и его мощность убывает по мере того, как в полосе тракта остается все меньшая доля его спектра.

Рассмотрим подробнее процесс обработки сигналов при использовании метода частичного разнесения в стационарном режиме и при установлении стационарного режима.

Стационарный режим. Обработка сигналов может быть иллюстрирована на укрупненной структурной схеме на рис. 26.1. Компенсаторы и заменим на блоки вычитания (-), удаление помех путем взаимной замены пораженных фрагментов спектра производится в блоках Ф1 и Ф2.

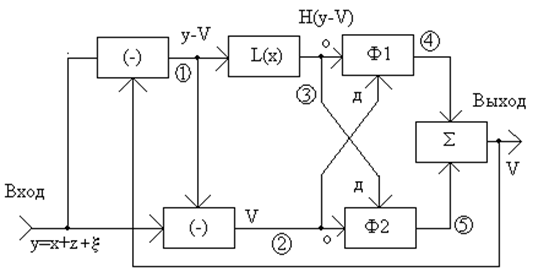Рис. 26.1.

Для краткости обозначим проведение операции L{x} через Lx. Также обозначим через h₁Åх и h₂Å х – операции, осуществляемые в блоках Ф1 и Ф2 соответственно, и приводящие к замене пораженных фрагментов в частотной или во временной области в основном сигнале (вход 0) на неповрежденные соответствующие фрагменты из другого разнесенного сигнала, подавленного на дополнительный вход (д).

Пример схемы, осуществляющий подобную замену, приведен на рис. 26.2, где обозначены соответственно, через ИНВ, РФ и К операции инвертирования, режекции узкополосной помехи и стробирования сигнала путем переключения коммутатора.

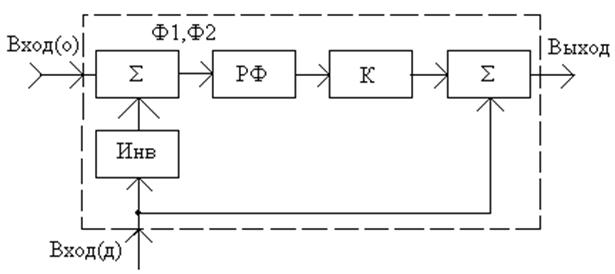Рис.26.2.

На входе действует сигнал у(t) = x(t)+z(t)+ξ, где z= Lx; ξ(t) – внешняя помеха. V(t) – сигнал на выходе. В точке 1 сигнал U₁=y-V; в точке 2 сигнал U₂=y-U₁=V; в точке 3 сигнал U₃=LU₁=L(y-V). Тогда в точке 4 будет сигнал U₄=h₁Å(U₃-U₂)+U₄; в точке 5 будет сигнал U₅=h₂Å(U₂-U₃)+U_2.

В сумматоре S суммарные сигналы U₄ и U₅ складываются (пусть с весовыми коэффициентами, равными 0,5), т.е. V=0,5 U₄+ 0,5U_5.

После соответствующих подстановок получим:

V=0,5{ h₁Å[L(y-V)-V]+V+h₂Å[V-L(y-V)]+(y-V)}.