Лекция 15. Угловые виды модуляции. Прямой и непрямой методы ЧМ модуляции. Фазовые модуляторы.
Колебание с постоянной амплитудой можно представить в общем виде как:
![]() (1.1)
(1.1)
где
![]() (1.2)
(1.2)
мгновенная фаза колебания u(t), ω – угловая частота колебания; φ0 – начальная фаза.
На рис.1.1 колебание вида (1.1) представлено вектором, длина которого равна амплитуде напряжения Uω . Вектор Uω вращается с угловой скоростью ω, увеличивая мгновенную фазу φ(t) (угол на который поворачивается вектор). Штриховой линией показано положение вектора в момент начала отсчета, когда φ(t) = φ0.
При угловой модуляции (УМ) вектор Uω вращается с переменной угловой скоростью, мгновенная фаза φ(t) растет не по линейному, а по сложному закону. Следовательно, при угловой модуляции возникает как частотная (ЧМ), так и фазовая (ФМ) модуляция. Таким образом, частотная и фазовая модуляции являются разновидностями угловой модуляции. При частотной и фазовой модуляции изменяются соответственно частота и фаза РЧ колебания пропорционально мгновенному значению передаваемого сигнала, а амплитуда модулированного колебания постоянна и не зависит от передаваемого сигнала. Из рис.1.1 видно, что ЧМ РЧ колебания сопровождается фазовой модуляцией этого колебания, и наоборот.
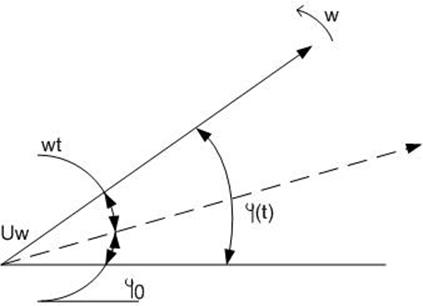
рис. 1.1
Из (1.2) следует, что частота ω связана с мгновенной фазой φ(t) колебания соотношением
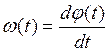 (1.3)
(1.3)
Если известна частота ω, то мгновенная фаза колебания
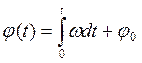 (1.4)
(1.4)
Если передается сигнал uΩ(t), то при ЧМ частота ВЧ колебания меняется по закону передаваемого сигнала:
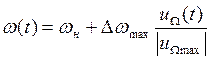 ,
(1.5)
,
(1.5)
где ![]() –
абсолютное максимальное значение сигнала, при котором обеспечивается
максимальное отклонение частоты при модуляции
–
абсолютное максимальное значение сигнала, при котором обеспечивается
максимальное отклонение частоты при модуляции ![]() ;
; ![]() - девиация частоты.
- девиация частоты.
При ФМ фаза ВЧ колебания меняется по закону передаваемого сигнала:
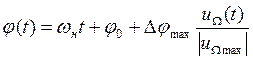 , (1.4)
, (1.4)
где ![]() –
девиация фазы.
–
девиация фазы.
Для составления аналитических выражений для ЧМ и ФМ колебаний рассмотрим сначала случай, когда несущее колебание модулируется гармоническим модулирующим сигналом с угловой частотой Ω и амплитудой UΩ.
При этом
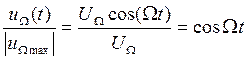
При ЧМ одним гармоническим колебанием частота модулированного РЧ колебания
![]() (1.7)
(1.7)
Из-за изменения частоты в ЧМ колебании меняется и мгновенная фаза этого колебания
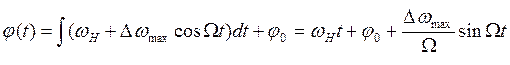 (1.8)
(1.8)
Сравнивая
(1.7) и (1.8), можно сделать вывод, что при изменении частоты РЧ – колебания по
косинусоидальному закону фаза такого колебания меняется по синусоидальному
закону. При этом ЧМ с девиацией частоты ![]() эквивалентна
ФМ с девиацией фазы
эквивалентна
ФМ с девиацией фазы
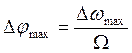 (1.9)
(1.9)
Для ЧМ РЧ – колебания с учетом (1.1) и (1.8) можно записать
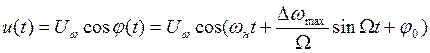 , (1.10)
, (1.10)
где 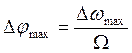 -
индекс ЧМ, прямо пропорционален амплитуде
-
индекс ЧМ, прямо пропорционален амплитуде ![]() гармонического
модулирующего сигнала и обратно пропорционален его угловой частоте Ω.
гармонического
модулирующего сигнала и обратно пропорционален его угловой частоте Ω.
При ФМ одним гармоническим колебанием фаза модулированного колебания изменяется по закону
![]() (1.11)
(1.11)
Тогда для РЧ – колебания при ФМ можно записать
![]() (1.12)
(1.12)
Частота такого колебания меняется по закону
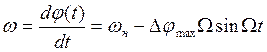 (1.13)
(1.13)
При этом ФМ с
девиацией фазы ![]() сопровождается ЧМ с девиацией
частоты
сопровождается ЧМ с девиацией
частоты
![]() (1.14)
(1.14)
Таким образом, общее для ЧМ и ФМ то, что модуляция одного из параметров РЧ – колебания неизбежно вызовет изменение другого параметра. Различие между ЧМ и ФМ в том, что при гармонической ЧМ девиация фазы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.