Лекция 32. Подавление комплекса узкополосных помех
Один из типичных вариантов помеховой обстановки – воздействие на систему связи с пространственным разнесением комплекса узкополосных помех от нескольких независимых источников. Подобная ситуация является в своем роде промежуточной между воздействием «гладких» помех, которые отличаются только амплитудой и фазовым сдвигом в различных ветвях разнесения, и общим случаем воздействия широкополосных помех, у которых частотная зависимость взаимно-корреляционной функции в полосе помехи проявляется достаточно явно.
Каждая сосредоточенная помеха является узкополосной, поэтому ее составляющие в разнесенных сигналах отличаются лишь амплитудой и фазовым сдвигом (т.е. каждая из таких помех по отдельности - «гладкая» – по аналогии с «гладкими» замираниями, порождающими лишь амплитудно-фазовые различия, в отличие от СЧЗ, порождающих частотно-селективные различия). В то же время каждый источник такой сосредоточенной помехи предполагается независимым от других источников помехи. Поэтому для разных сосредоточенных помех, расположенных в различных участках спектра, взаимные амплитудно-фазовые соотношения тоже различаются.
Это сближает с ситуацией воздействия широкополосных помех с частотно-зависимыми (в общем случае) соотношениями между спектральными составляющими в различных ветвях разнесения. То есть комплекс сосредоточенных помех, рассматриваемый в целом в полосе сигнала, может считаться, как одна широкополосная помеха. Однако такая помеховая ситуация имеет свою специфику, позволяющую отойти от общего труднореализуемого оптимального алгоритма объединения с частотно-зависимыми весовыми функциями и реализовать более простую квазиоптимальную обработку. В реальности сосредоточенные помехи, входящие в комплекс, редко накладываются по частотной оси одна на другую из-за узкополосности их спектров.
Пусть на систему воздействует М узкополосных помех с полосами спектра, равными ППj, j=1¸M. (Нумерацию источников договоримся осуществлять с учетом ранжирования ширины полос, т.е. ПП1³ПП2³…³ППМ). Здесь предполагается, что источники помех не являются адаптивными постановщиками [62,80,81,87], осуществляющими нацеливание помехи на информационный сигнал для его эффективного подавления, т.е. местоположение помехи в полосе сигнала случайно и независимо у разных источников.
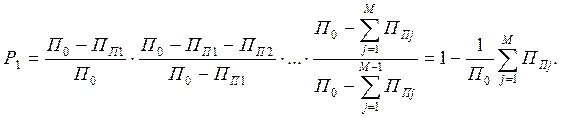 |
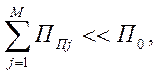 |
|||
- может появиться возможность компенсировать комплекс из М узкополосных помех системой с кратностью разнесения N<M (вплоть до двукратного разнесения);
- в общей полосе сигнала могут присутствовать области, свободные от помех, что облегчит определение нужных для комбинирования величин весовых коэффициентов.
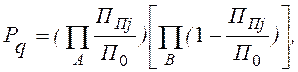 |
Тогда вероятность поражения частоты fqбудет равна где произведения берутся по номерам j, включенным при данных вариантах разбиения в множества А и В.
Вероятность Pq зависит от варианта разбиения набора М на А и В, а общее число вариантов равно 2М. В случае, если можно считать ширину полос всех помех одинаковой (например, приравнивая их к максимальной ПП1), то вероятность совпадения с частотой fq полос m сигналов помех будет равна
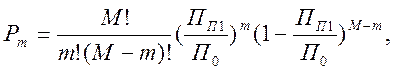 |
Система с N-кратным разнесением может полностью подавлять помехи от М источников на любой частоте в
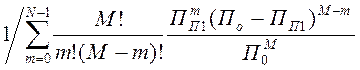 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.