Подавление комплекса узкополосных помех, страница 2

На выходе корреляционного компенсатора соотношение  полезного сигнала к помехе равно величине, обратной этому соотношению на его опорном входе. Рассмотрим ситуацию двукратного разнесения и воздействия помехи от одного источника. Поскольку полезный сигнал x(t)=mx₀(t) и помеха y(t)=hy₀(t), (<x₀²>=<y₀²>=1)  взаимно независимы, их можно условно расположить вдоль осей OX и OY некоторой системы координат (см. рис. 1). Разнесенные сигналы S₁ и S₂в результате аддитивного действия помехи являются  линейными   комбинациями сигналов x₀(t) и y₀(t), то есть   в этой системе координат их можно описать некоторыми векторами ОС и ОА.

В любом из корреляционных компенсаторов (КК) из напряжения на его сигнальном входе (пусть S₁) вычитается  с определенным весовым коэффициентом  k сигнал на  его опорном входе (S₂). Величина коэффициента k автоматически устанавливается таким образом, чтобы выходной сигнал компенсатора S₄=S₁+kS₂ стал некоррелирован  с сигналом  S₂.

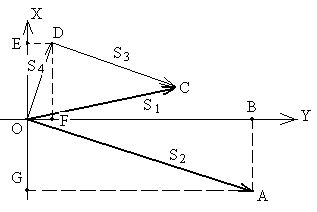Сигнал S₁  можно в векторной форме представить как сумму двух взаимно-перпендикулярных  векторов S₃ и S₄. Один из них параллелен вектору S_2, другой – перпендикулярен S₂ (т.е. с ним некоррелирован). В результате работы КК компонент S₃ удаляется. Оставшийся компонент (вектор S₄) ортогонален вектору S₂.

Таким образом, рассматривая треугольники ОАВ и ОFD, нетрудно установить пропорцию: ОВ/ОG=OE/OF. Но OB/OG=r₂ – соотношение уровней полезного сигнала и помехи в опорном сигнале S₂; OF/OE = r₄ – соотношение уровней сигнала в выходном сигнале S₄. При этом r₂=1/r₄.

В случае, если в опорном напряжении составляющие полезного сигнала x(t) отсутствуют, в выходном сигнале  S₄(t) будут отсутствовать помеховые составляющие, т.е. произойдет полная компенсация помехи (и, наоборот, при отсутствии в опорном  напряжении составляющих помехи, на выходе КК   произойдет компенсация полезного сигнала). Это объясняется тем, что помеховые составляющие «не будут мешать» компенсатору определять нужные значения коэффициента k.

Этот факт можно использовать в рассматриваемых условиях помеховой обстановки следующим образом. Воздействие комплекса узкополосных помех оставляет некоторые области спектра полезного сигнала свободными от спектральных составляющих помехи. В то же время в отсутствие селективно-частотных замираний полезного сигнала амплитудно-фазовые соотношения полезных компонент в разнесенных сигналах одинаковы для всей полосы спектра полезного сигнала. Поэтому, если потребуется  компенсировать полезную составляющую разнесенных сигналов, то нет необходимости измерять необходимые для этого амплитудно-фазовые соотношения во всей полосе полезного сигнала. Достаточно их измерить только в областях полосы, не пораженных помехами. Результат такого измерения будет в равной мере относиться и к пораженным областям сигнала.

Подобный факт дает возможность процедуру удаления помех производить в два этапа. На первом этапе в некотором вспомогательном  сигнале S_В компенсируются полезные составляющие. При этом необходимые для компенсации амплитудно-фазовые соотношения определяются в областях, где отсутствуют узкополосные помехи. В результате в S_B будет присутствовать только набор узкополосных помех.

На втором этапе производится раздельная компенсация каждой из помех, поскольку предполагается, что они порождены различными источниками и имеют различающиеся амплитудно-фазовые соотношения в ветвях разнесения. Сумма помех расфильтровывается, образуя набор из М напряжений, каждое из которых является отдельной помехой. Эти  напряжения с помощью корреляционных компенсаторов поочередно  вычитаются из входных сигналов, последовательно очищая их от помех.

Реализация предложенного принципа для двукратного разнесения поясняется рис. 32.2 а),б),в) и в виде структурной схемы приведена на рис.32.3.

На рис. 2 а) изображены спектры двух разнесенных сигналов (I и II), содержащие полезные компоненты и комплекс сосредоточенных помех (1 и 2). На рис. 32.2 б) изображена форма спектра полезного сигнала после режектирования помех, она используется для определения необходимых соотношений между полезными сигналами. На рис.32.2 в) представлен комплекс помех, который будет далее расфильтровываться.

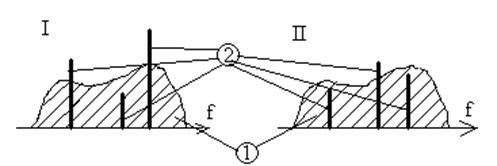Рис.32.2 а)