Ознакомление с симплексным методом и методом случайного поиска оптимальных параметров и экстремума целевой функции

Цель работы: ознакомление с симплексным  методом и методом случайного поиска оптимальных параметров и экстремума целевой функции, а также изучение свойств этих методов.

1 Исходные данные:

1.1 Целевая функция ,

1.2 Оптимальные значения параметров х₁ и х₂, рассчитанные методом Гаусса-Зейделя, при которых функция имеет локальный максимум, равны х₁=8, х₂=4, при этом значение целевой функции равно у=30,2.

2 Оптимизация методом случайного поиска

2.1 Выбираем начальную точку х₁₀= х₂₀=20.

2.2 Выбираем интервалы варьирования Δх₁=1; Δх₂=1; размер случайного вектора ρ_{сл п}=10, шаг а_{сл п}=12 (в нормированных единицах).

2.3 Определяем составляющую ξ₁  случайного вектора ξ и ее знак по таблице равномерно распределенных случайных чисел из интервала (0; 10). Начало отсчета в таблице – I случайное число. Составляющую ξ₂ находим по формуле

2.4 Находят координаты пробной точки, вычисляем значение функции у в данной и начальной точках, сравниваем их.

2.5 Далее совершаем рабочий шаг в новую начальную точку в соответствии с полученными откликами.

2.6 В точках на окружности радиусом ρ_{сл п}=10 с нормированными координатами A (x₀- ρ_{сл п}, y₀), B (x₀+ ρ_{сл п}, y₀), C (x₀, y₀- ρ_{сл п}), D (x₀, y₀+ ρ_{сл п}) вычисляем значения целевой функции для определения момента, когда во все стороны от базовой точки отклики оказываются меньше, чем в ней самой.

2.7 Повторяем шаги 2.3-2.6 до тех пор, пока во все стороны от начальной точки отклики оказываются меньше, чем в ней самой.

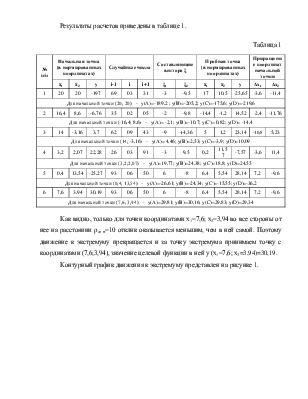
Результаты расчетов приведены в таблице 1.

Таблица 1

Как видно, только для точки координатами х₁=7,6; х₂=3,94 во все стороны от нее на расстоянии ρ_{сл п}=10 отклик оказывается меньшим, чем в ней самой. Поэтому движение к экстремуму прекращается и за точку экстремума принимаем точку с координатами (7,6;3,94), значение целевой функции в ней у (х₁=7,6; х₂=3,94)=30,19.

Контурный график движения к экстремуму представлен на рисунке 1.

3 Оптимизация симплексным методом

3.1 Выбираем начальную точку х₁₀= х₂₀=16.

3.2 Выбираем интервалы варьирования Δх₁=2; Δх₂=2; безразмерная величина стороны ρ_сим=1(регулярный симплекс). Для n = 2 имеем ρ » 0,966, q » 0,259.

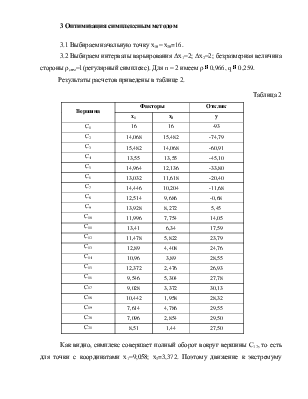
Результаты расчетов приведены в таблице 2.

Таблица 2

Как видно, симплекс совершает полный оборот вокруг вершины С₁₇, то есть для точки с координатами х₁=9,058; х₂=3,372. Поэтому движение к экстремуму прекращается и за точку экстремума принимаем точку с координатами (9,058;3,372), значение целевой функции в ней у (х₁=9,058; х₂=3,372)=30,13.

Контурный график движения к экстремуму представлен на рисунке 2.

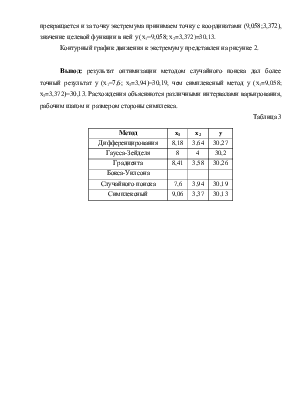
Вывод: результат оптимизации методом случайного поиска дал более точный результат у (х₁=7,6; х₂=3,94)=30,19, чем симплексный метод у (х₁=9,058; х₂=3,372)=30,13. Расхождения объясняются различными интервалами варьирования, рабочим шагом и  размером стороны симплекса.

 Таблица 3