
Цель работы: изучение методики определения корреляционной связи между параметрами.
Содержание работы:
1) Определение корреляционной связи между выходной проводимостью транзистора при холостом ходе в цепи эмиттера и начальным током коллектора при отсутствии тока эмиттера;
2) Нахождение доверительного интервала для коэффициента корреляции.
Исходные значения параметров:
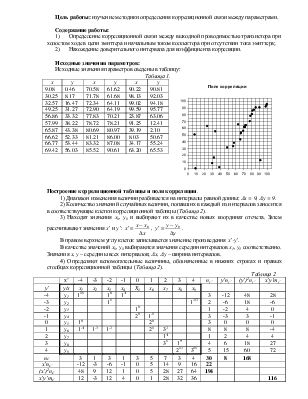
Исходные значения параметров сведены в таблицу:
Таблица 1.
|
x |
y |
x |
y |
x |
y |
|
|
9.08 |
0.46 |
70.58 |
61.62 |
90.22 |
90.81 |
|
|
30.25 |
8.17 |
71.78 |
61.68 |
98.13 |
92.03 |
|
|
32.57 |
16.47 |
72.34 |
64.11 |
99.02 |
94.18 |
|
|
49.25 |
31.27 |
72.90 |
64.19 |
99.59 |
95.77 |
|
|
56.86 |
33.32 |
77.83 |
70.21 |
23.87 |
63.06 |
|
|
57.99 |
38.22 |
78.72 |
78.21 |
91.25 |
12.41 |
|
|
65.87 |
43.38 |
80.69 |
80.97 |
39.19 |
2.10 |
|
|
66.62 |
52.33 |
81.21 |
86.00 |
8.03 |
50.67 |
|
|
66.77 |
53.44 |
83.32 |
87.08 |
34.17 |
55.24 |
|
|
69.42 |
56.03 |
85.52 |
90.61 |
63.20 |
65.53 |
|
Построение корреляционной таблицы и поля корреляции.
1) Диапазон изменения величин разбивается на интервалы равной длины: Dx = 9, Dy = 9.
2) Количество значений случайных величин, попавших в каждый из интервалов заносится в соответствующие клетки корреляционной таблицы (Таблица 2).
3) Находят
значения x0, y0 и выбирают их в качестве новых
координат отсчета. Затем рассчитывают значения x’
и y’: 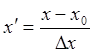 ,
, 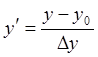 .
.
В правом верхнем углу клеток записывается значение произведения x’×y’.
В качестве значений x0, y0 выбираются значения середин интервалов x3, y3 соответственно. Значения x, y – середины всех интервалов; Dx, Dy – ширина интервалов.
4) Определяют вспомогательные величины, обозначенные в нижних строках и правых столбцах корреляционной таблицы (Таблица 2).
|
x’ |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
ny’ |
y’ny’ |
(y’)2ny’ |
x’y’my’ |
|
|
y’ |
y/x |
x1 |
x2 |
x3 |
x4 |
X5 |
x6 |
x7 |
x8 |
x9 |
||||
|
-4 |
y1 |
116 |
18 |
14 |
3 |
-12 |
48 |
28 |
||||||
|
-3 |
y2 |
16 |
1-12 |
2 |
-6 |
18 |
-6 |
|||||||
|
-2 |
y3 |
10 |
1 |
-2 |
4 |
0 |
||||||||
|
-1 |
y4 |
20 |
1-1 |
3 |
-3 |
3 |
-1 |
|||||||
|
0 |
y5 |
10 |
20 |
3 |
0 |
0 |
0 |
|||||||
|
1 |
y6 |
1-4 |
1-3 |
1-2 |
21 |
32 |
8 |
8 |
8 |
-4 |
||||
|
2 |
y7 |
14 |
1 |
2 |
4 |
4 |
||||||||
|
3 |
y8 |
36 |
19 |
4 |
6 |
18 |
27 |
|||||||
|
4 |
y9 |
212 |
316 |
5 |
15 |
60 |
72 |
|||||||
|
nx’ |
3 |
1 |
3 |
1 |
3 |
5 |
7 |
3 |
4 |
30 |
8 |
168 |
||
|
x’nx’ |
-12 |
-3 |
-6 |
-1 |
0 |
5 |
14 |
9 |
16 |
22 |
||||
|
(x’)2nx’ |
48 |
9 |
12 |
1 |
0 |
5 |
28 |
27 |
64 |
194 |
||||
|
x’y’mx’ |
12 |
-3 |
12 |
4 |
0 |
1 |
28 |
32 |
36 |
116 |
Расчет коэффициента корреляции, оценка его достоверности.
Эмпирический коэффициент корреляции r*xy находится по формуле:
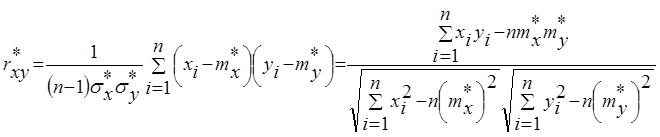
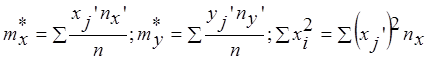 ,
, 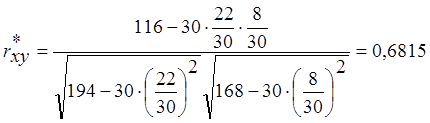
Определение доверительного интервала коэффициента корреляции:
Среднеквадратическое отклонение коэффициента корреляции (при n ³ 30) определяется по формуле:
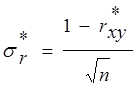 ,
, 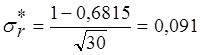 ;
;
доверительный интервал находят из выражения:
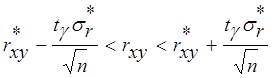 , где tg
- коэффициент распределения Стьюдента, определяемый по таблицам распределения
Стьюдента в зависимости от принятой доверительной вероятности g и числа степеней свободы n-1.
, где tg
- коэффициент распределения Стьюдента, определяемый по таблицам распределения
Стьюдента в зависимости от принятой доверительной вероятности g и числа степеней свободы n-1.
При g=0,8, tg=1,31 доверительный интервал имеет вид:
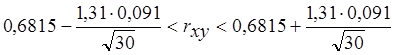
![]()
Вывод: С помощью методики определения корреляционной связи между параметрами были расчитаны:
- коэффициент корреляции r*xy=0.6815
- среднеквадратическое отклонение коэффициента корреляции s*R = 0.091
-
доверительный
интервал коэффициента корреляции ![]() .
.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.