Ознакомление с градиентным методом и методом Бокса-Уилсона поиска оптимальных параметров и экстремума целевой функции

Цель работы: ознакомление с градиентным методом и методом Бокса-Уилсона поиска оптимальных параметров и экстремума целевой функции, а также изучение свойств этих методов.

1. Исходные данные:

1.1 Целевая функция ,

1.2 Начальная точка при оптимизации х_i0=x_i0+22, где x_i – заданные значения начальной точки x₁₀ = х₂₀ = -2;

1.3 Оптимальные значения параметров х₁ и х₂, рассчитанные методом Гаусса-Зейделя, при которых функция имеет локальный максимум, равны х₁=8, х₂=4, при этом значение целевой функции равно у=30,2.

2 Оптимизация обычным методом градиента

2.1 Выбираем базовую точку х₁₀=20, х₂₀=20.

2.2 Выбираем интервалы варьирования Δх₁=1; Δх₂=1; рабочий шаг ρ=1.

2.3 Определяем координаты пробных точек, находим значений функции в каждой из них.

2.4 Вычисляем оценки а_i составляющих вектор-градиента в начальной точкедля каждого i-го фактора по формуле

grad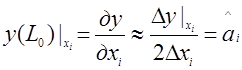

2.5 Находим координаты рабочей точки на направлении градиента:

Эту точку принимаем за новую базовую.

2.6 Повторяем шаги 2.3-2.5 до тех пор, пока на очередном шаге все составляющие не станут пренебрежимо малыми, для этого достаточно, чтобы выполнялось неравенство < 1.

Результаты расчетов приведены в приложении.

По результатам пробных опытов в восьмой рабочей точке условие пункта 2.6 выполняется, поэтому движение к экстремуму прекращается и за точку экстремума принимаем точку .

Иллюстрация градиентного метода представлена на рисунке 1.