3 Нахождение оптимальных параметров и экстремума целевой функции методом линейного
Задание: предприятие должно выпустить два вида продукции, используя последовательно четыре различных группы производственного оборудования. Выпуск одного комплекта продукции вида А обеспечивает прибыль в два миллиона рублей, продукции вида В – в три миллиона рублей. Месячный фонд времени, в днях, каждой группы оборудования и трудоемкость, также в днях, для изготовления комплектов продукции А и В представлены в таблице 2. Разработать план производства, который обеспечит наибольшую прибыль для предприятия.
Таблица 2.
|
Группа оборудования |
Норма времени на выпуск одного комплекта продукции |
Фонд времени |
|
|
А |
В |
||
|
I |
3,8 |
3,8 |
15,8 |
|
II |
2,8 |
5,2 |
18 |
|
III |
3,2 |
0,8 |
16 |
|
IV |
1,8 |
2,8 |
8,8 |
Вначале составляется целевая функция (целевая функция – прибыль):
y=2x1+3x2, где x1 – количество комплектов продукции вида А,
x2 – количество комплектов продукции вида B.
Уравнения
ограничений:
3,8x1+3,8x2 ≤15,8
2,8x1+2,8x2 ≤18
3,2x1+3,2x2 ≤16
1,8x1+2,8x2 ≤8,8
Здесь x1≥0, x2≥0.
Строятся линии ограничений по уравнениям ограничений (таблица 3).
Таблица 3
|
Номер уравнения ограничений |
Первое решение |
Второе решение |
||
|
x1 |
x2 |
x1 |
x2 |
|
|
1 |
0 |
4,2 |
4,2 |
0 |
|
2 |
0 |
6,4 |
6,4 |
0 |
|
3 |
0 |
5 |
5 |
0 |
|
4 |
0 |
3,1 |
4,8 |
0 |
Определяется область ограничений (рисунок 5).
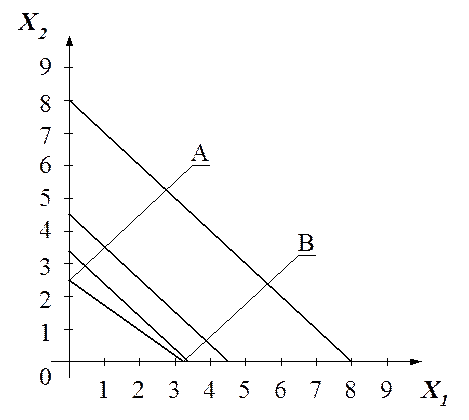
Рисунок 5 - Линии ограничений
Точки А и В ограничивают область возможных значений целевой функции. Для нахождения максимального значения целевой функции находятся ее значения в точках А (0; 3,1), В (4,2; 0) и С (4,1; 0,6).
yA=2×0+3×3,1=9,3 млн.руб.
yВ=2×4,2+3×0=8,4 млн.руб.
yС=2×4,1+3×0,6=6 млн. руб.
Т.о. наибольшего значения целевая функция прибыли достигает в точке А при значениях параметров x1=0, x2=3,1.
Так как количество комплектов оборудования не может быть выражено дробным числом, то нужно округлить значения x1 и x2 до целых чисел, а затем выполнить проверку.
Округляется значение параметра x2:
1) Пусть x1=0, x2≈4, тогда
3,8×0+3,8×4=15,2<15,8 – верно;
2,8×0+2,8×4=11,2<18 – верно;
3,2×0+3,2×4=12,8<16 – верно;
1,8×0+2,8×4=11,2>8,8 – неверно.
Одно из ограничений не выполняется, поэтому значение параметра x2 нужно округлять до меньшего целого.
2) Пусть x1=0, x2≈3, тогда:
3,8×0+3,8×3=11,4<15,8 – верно;
2,8×0+2,8×3=8,4<18 – верно;
3,2×0+3,2×3=9,6<16 – верно;
1,8×0+2,8×3=8,4<8,8 – верно.
Все ограничения выполняются.
Округляется значение параметра x1:
1) Пусть x1≈4, x2=0, тогда:
3,8×4+3,8×0=15,2<15,8 – верно;
2,8×4+2,8×0=11,2<18 – верно;
3,2×4+3,2×0=12,8<16 – верно;
1,8×4+2,8×0=7,2<8,8 – верно.
Все ограничения выполняются.
Целевая функция при этом принимает значение
yA=2×0+3×3=9 млн.руб.;
yВ=2×4+3×0=8 млн.руб.
Следовательно, при округлении до меньшего целого значения параметра x2, либо параметра x1 значения целевой функции в точках А и В оказались разными.
Таким образом, в соответствии с расчётами план производства, который обеспечит предприятию наибольшую прибыль – это выпуск четырех комплектов продукции вида В или трех комплектов продукции вида А в зависимости от спроса. При этом прибыль предприятия составит 9 млн. руб. или 8 млн. руб. соответственно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.