ГЛАВА «ЧИСЛОВАЯ СИСТЕМА»
Числа {1,2,3,… }, получающиеся из единицы операцией
сложения называют натуральными и обозначают ![]() . Геометрическая интерпретация натуральных
чисел --точки на прямой ℓ, которые получаются в результате откладывания с
помощью циркуля выбранного заранее единичного отрезка в выбранном направлении.
Такой интерпретацией мы далее будем пользоваться постоянно, поэтому
сформулируем
. Геометрическая интерпретация натуральных
чисел --точки на прямой ℓ, которые получаются в результате откладывания с
помощью циркуля выбранного заранее единичного отрезка в выбранном направлении.
Такой интерпретацией мы далее будем пользоваться постоянно, поэтому
сформулируем
Определение. Числовой осью ![]() называется
прямая ℓ, с выбранной на ней точкой O (начало отсчета), выбранном
положительном направлении и выбранном отрезке
называется
прямая ℓ, с выбранной на ней точкой O (начало отсчета), выбранном
положительном направлении и выбранном отрезке ![]() , длину
которого полагаем равным единице.
, длину
которого полагаем равным единице.
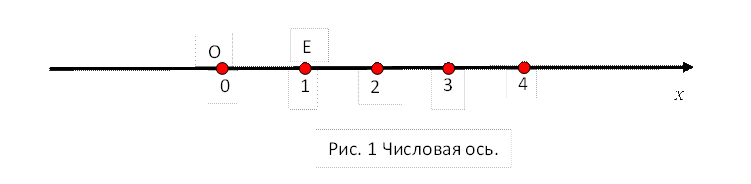
Итак, мы начали приписывать точке ![]() на оси
координату
на оси
координату ![]() – число. Сейчас мы это сделали только для
некоторых точек – концов отрезков
– число. Сейчас мы это сделали только для
некоторых точек – концов отрезков ![]() .
.
Присоединим к множеству натуральных чисел элемент ноль 0,
обладающий свойствами ![]()
![]() для любого
для любого ![]() . Получаем множество
. Получаем множество ![]() всех целых неотрицательных чисел. Именно
началу координат, точке
всех целых неотрицательных чисел. Именно
началу координат, точке ![]() припишем нулевую координату.
припишем нулевую координату.
На множестве ![]() 0 имеется отношение линейного
порядка. Скажем, что n<m, (n строго меньше m), если найдется натуральное число k такое, что
0 имеется отношение линейного
порядка. Скажем, что n<m, (n строго меньше m), если найдется натуральное число k такое, что ![]() . Геометрически
это значит, что точка, соответствующая числу m лежит правее точки,
соответствующей числу n. Отношение
. Геометрически
это значит, что точка, соответствующая числу m лежит правее точки,
соответствующей числу n. Отношение ![]() нестрогого неравенства тогда получается из
отношения строгого неравенства простой логической операцией: n≤ m по
определению означает, что либо n=m, либо n<m. Например, 5≤ 5 -- верное
высказывание.
нестрогого неравенства тогда получается из
отношения строгого неравенства простой логической операцией: n≤ m по
определению означает, что либо n=m, либо n<m. Например, 5≤ 5 -- верное
высказывание.
Операция деления не всегда возможна в области натуральных
чисел. Это дает нам право ввести отношение делимости: скажем, что число n
делит число m, если ![]() для какого-либо подходящего k∈
для какого-либо подходящего k∈![]() . Обозначается это отношение так:
. Обозначается это отношение так: ![]() . Среди всех натуральных чисел особо
выделяются простые числа -- это числа p имеющие ровно
два делителя -- единицу и само число p. Первые
несколько простых чисел таковы:
. Среди всех натуральных чисел особо
выделяются простые числа -- это числа p имеющие ровно
два делителя -- единицу и само число p. Первые
несколько простых чисел таковы:
![]()
Множество простых чисел бесконечно.
Основная теорема арифметики гласит, что любое натуральное
число большее единицы разложимо в произведение простых чисел и это разложение
единственно с точностью до перестановки сомножителей. Например, ![]() есть разложение на простые множители числа
120.
есть разложение на простые множители числа
120.
На множестве натуральных чисел уравнение вида ![]() не разрешимо, вообще говоря, относительно
не разрешимо, вообще говоря, относительно ![]() . Чтобы
исправить это, вводятся отрицательные целые числа. Это множество {-1,-2,-3,… }.
Считаем, что 0>-1>-2>-3>… и, таким образом, по определению
неравенство -k>-m для двух натуральных чисел k и m имеет место тогда и
только тогда, когда k<m. Совокупность как положительных так и отрицательных
целых чисел, а также нуля называется кольцом целых чисел ℤ . Итак:
. Чтобы
исправить это, вводятся отрицательные целые числа. Это множество {-1,-2,-3,… }.
Считаем, что 0>-1>-2>-3>… и, таким образом, по определению
неравенство -k>-m для двух натуральных чисел k и m имеет место тогда и
только тогда, когда k<m. Совокупность как положительных так и отрицательных
целых чисел, а также нуля называется кольцом целых чисел ℤ . Итак:
![]()
Термин "кольцо" значит, что на этом множестве имеются операции сложения и умножения, подчиняющиеся свойствам перестановочности (коммутативности), сочетательности (ассоциативности) и распределительному закону (дистрибутивность), а также для любого числа имеется противоположное, в сумме с которым данное число дает ноль – нейтральный элемент операции сложения.
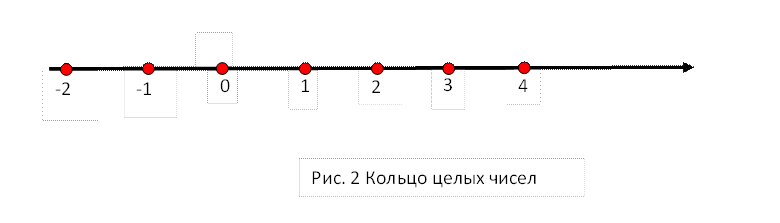
Целые отрицательные числа интерпретируются на числовой оси точками, которые получаются откладыванием единицы масштаба в отрицательном направлении (см. рис. 2)
Для целых чисел отношение делимости вводится также как и для натуральных чисел.
Евклидовость кольца целых чисел заключается в том, что для любого ненулевого числа n и для любого целого числа m найдутся единственные числа q (неполное частное) и r (остаток) такие, что
![]()
Для целых чисел a,b,c,… определяются наибольший общий делитель НОД(a,b,c,… ) как наибольший из общих делителей этих чисел, а также наименьшее общее кратное НОК(a,b,c,… ), как наименьшее неотрицательное целое число, которое делится на каждое из чисел a,b,c,… . Числа a,b,c,… называются взаимно простыми, если НОД(a,b,c,… )=1. Вычислим
НОД(30,48)=6; НОК(30,48)=48⋅ 30/6=30⋅ 8=240
Здесь мы воспользовались формулой
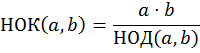
Очень часто требуется разделить некоторую величину на n
равных частей, т.е. решить уравнение ![]() . В кольце целых чисел
такое уравнение не всегда разрешимо, и мы вновь встаем перед проблемой
расширения системы чисел до более обширной, в которой сохраняются прежние
алгебраические правила, и данное уравнение всегда разрешимо при
. В кольце целых чисел
такое уравнение не всегда разрешимо, и мы вновь встаем перед проблемой
расширения системы чисел до более обширной, в которой сохраняются прежние
алгебраические правила, и данное уравнение всегда разрешимо при ![]() .
Рациональное число есть дробь вида
.
Рациональное число есть дробь вида ![]() , где знаменатель
, где знаменатель ![]() есть
целое число, отличное от 0, а числитель
есть
целое число, отличное от 0, а числитель ![]() -- произвольное целое число. Считаем
-- произвольное целое число. Считаем
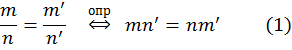
Отсюда следует правило сокращения: ![]() . Операции сложения и умножения над
дробями определяются так
. Операции сложения и умножения над
дробями определяются так
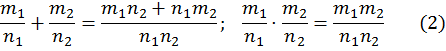
Относительно этих операций множество всех рациональных чисел
![]() образует поле, т.е. помимо законов
ассоциативности, коммутативности и дистрибутивности
образует поле, т.е. помимо законов
ассоциативности, коммутативности и дистрибутивности
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.