Дифференциальные уравнения. Задачи, приводящие к дифференциальным уравнениям

Понятие линейной зависимости понадобится нам и для функций.

Функции  называются  линейно  зависимыми, если найдутся константы   не все равные 0 и такие,  что . В противном случае эти функции называются  линейно независимыми. Иными словами, функции  линейно независимы, если из соотношения     вытекают равенства  

Линейная независимость двух функций равносильна тому, что их отношение не равно константе. Действительно, если  и, скажем, , то  Наоборот, если , то  соотношение  будет нетривиальной линейной зависимостью. Например, функции  линейно зависимы, так как вторая получается из первой умножением на  C другой стороны степенные функции  линейно независимы. Докажем это. Пусть

Дифференцируя это соотношение по  n-1 раз, получим

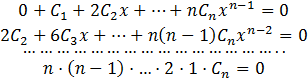
Подставляя в эту систему, а также в уравнение (2) вместо  ноль, получаем: .

Предложение. Определитель Вронского линейно зависимых функций равен тождественно нулю.

Теорема (формула Лиувилля).  Пусть  есть решения однородного линейного дифференциального уравнения . Обозначим через  значение определителя Вронского этой системы функций в фиксированной точке  Тогда

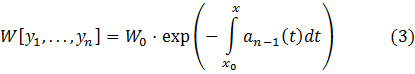
Следствие. Если в условиях теоремы , то определитель Вронского тождественно равен нулю и функции  линейно зависимы.

Доказательство проведем только для n=2. Имеем:

Пусть  есть частные решения дифференциального уравнения   Тогда  откуда  Аналогично,  Следовательно,

Решая дифференциальное уравнение с разделяющимися переменными  получим формулу Лиувилля (3).

Докажем теперь следствие. Тот факт, что  тождественно вытекает сразу из формулы Лиувилля (3).   Линейную зависимость функций    докажем сначала в общем случае с использованием теоремы существования и единственности, а затем докажем в частном случае  без использования этой теоремы.

Итак, пусть  Тогда столбцы числового определителя  линейно зависимы, т.е. найдутся константы  не все равные 0 и такие, что

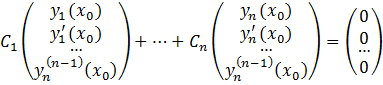
Рассмотрим частное решение  однородного дифференциального уравнения  . Так как

для , то получаем нулевые начальные условия у функции . Но  нулевая функция также имеет нулевые начальные условия.  Применяя теорему единственности, находим, что  и тем самым  есть нетривиальная линейная зависимость.

Теперь рассмотрим случай двух функций-решений дифференциального уравнения  Предполагаем  Из формулы Лиувилля вытекает, что . Тогда

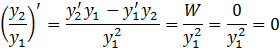
и  (см. раздел «Неопределенный интеграл»). Следовательно, функции линейно зависимы. □

Заметим, что мы попутно получили формулу

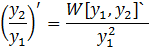
для двух функций, которую можно использовать для понижения порядка однородного дифференциального уравнения, у которого известно одно решение.

Пример.  Решим дифференциальное уравнение . Ищем решение  в виде степенной функции   Подставляя, получаем:

Итак, функция  есть решение заданного дифференциального уравнения.  Второе решение  находим из формулы   как

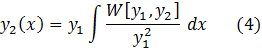
По формуле Лиувилля найдем сначала определитель Вронского:

Полагая  и применяя (4), находим

Взяв конкретное значение , получаем второе решение  не зависимое с первым.  Тем самым  будет общим решение заданного дифференциального уравнения (см. следующую теорему)

Набор n линейно независимых решений однородного дифференциального  уравнения порядка n называется  фундаментальной системой решений (сокращенно Ф.С.Р.)

Основная теорема о структуре пространства решений однородного линейного дифференциального уравнения. Пусть -- ф.с.р. однородного дифференциального уравнения. Тогда  есть общее решение этого уравнения.

Доказательство. В силу теоремы 1 предыдущего параграфа остаётся доказать, что для любых начальных условий  найдутся константы  такие, что  – решение задачи Коши с заданными начальными условиями. Это следует из того, что система линейных уравнений

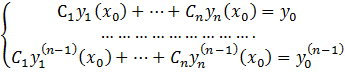
(относительно ) определена, так как её определитель есть в точности определитель Вронского  в точке  который не равен 0 в силу следствия формулы Лиувилля.

11  Линейные уравнения второго порядка с постоянными коэффициентами

Определение. Функция вида , где  -- комплексное число, а  -- многочлен