c.2.2 Записать алгоритм ДПФ в аналитической, матричной и Z-формах для ДП x(n), n[0;47].
Решение:
1)
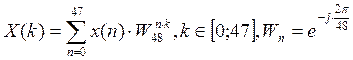
2)
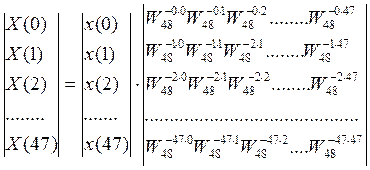
Или
3)
,
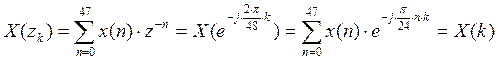Т.е. Z-преобразование в k=48 точках, равномерно расположенных на единичной окружности
с интервалом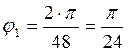 
, что соответствует отсчетам X(k) с дискретностью по оси частот 
.
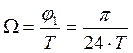С 2.3 Найти в форме ДПФ спектр последовательности единичных импульсов при N=12. Вычислить ОДПФ.
Решение.
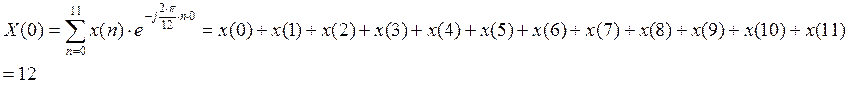
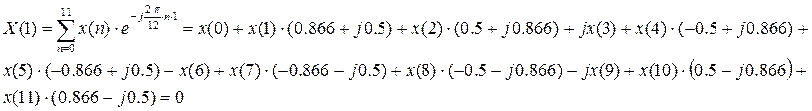
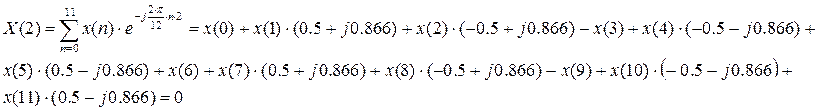
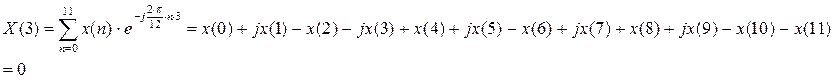
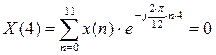
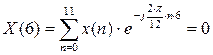
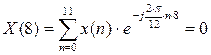
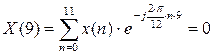
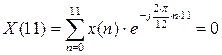
ОДПФ:
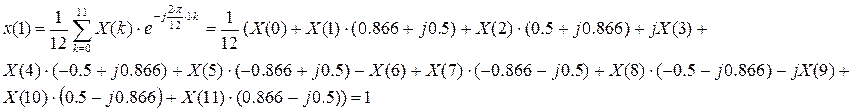
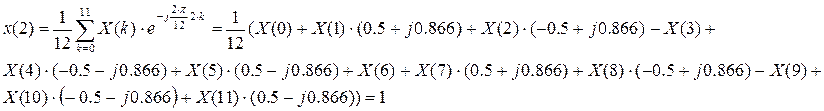
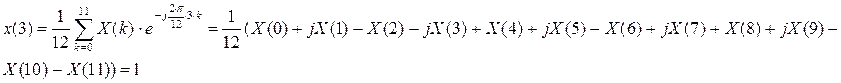
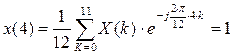
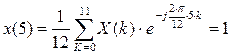
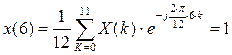
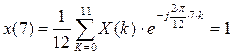
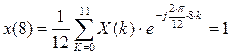
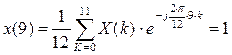
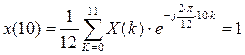
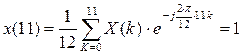
C2.4 Вычислить ДПФ, определить амплитудный и фазовый спектры последовательности x(n). 1,1,1,0.
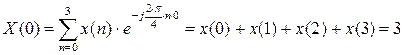
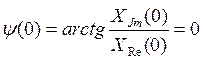
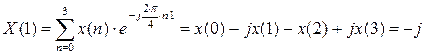
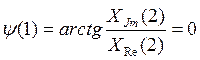
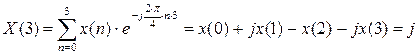
С 2.6 Определить длительность вычисления ДПФ и БПФ при N=4096, если процессор ЭВМ выполняет операцию комплексного
умножения за 
, а операцию сложения за 
. Определить выигрыш от использования БПФ.
Построить график выигрыша затрат при использовании БПФ различной размерности.
Длительность ДПФ и БПФ определяется более длительной операцией умножения. Поэтому:
|
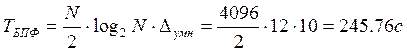
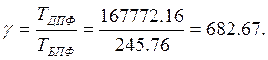
log2N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
γ |
4 |
4 |
5.3 |
8 |
12.8 |
21.3 |
36.6 |
64 |
113.8 |
204.8 |
372.4 |
682.7 |
С 2.7. Определить период дискретизации по частоте для ДПФ при N=16,32,64; T=0.5мс.
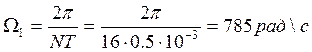
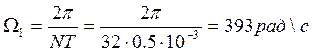
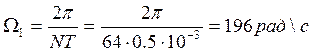
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
