Неопределенный интеграл. Свойства неопределенного интеграла. Классы интегрируемых функций. Замена переменной в неопределенном интеграле

Функции имеющие не более конечного числа разрывов 1-го рода на отрезке [a,b]. (их называют кусочно-непрерывными)

3.  Функции монотонные на отрезке [a,b] (у функции этого класса число разрывов может быть бесконечным).

1) Если  непрерывна на , то она интегрируема (ограничена).

2) Если ограниченная функция  на  имеет лишь конечное число точек разрыва, то она интегрируема на .

3) Монотонная ограниченная функция  всегда интегрируема.

Th1. Пусть надо вычислить н.и. . Если функция  дифференцируема на  и  интеграл  на промежутке , тогда (1)   на .

Формулу (1) часто записывают в виде:

 (1)’

После вычисления интеграла справа, вместо t подставим .Формулы (1) и (1)’ получаются, если бы мы ввели вместо переменную t, .

Пример:

Th2. Пусть надо вычислить интеграл . Если некоторая функция  дифференцируема на  и  на , то (2)

В формуле (2) мы формально вводим новую функцию .

Всякая рациональная дробь представима в виде  .

Если m≥n – дробь неправильная, выделяем целую часть : .

Всякую правильную рац. дробь, знаменатель которой разложен на множители , (множители  должны быть неразложимыми т.е. ), можно представить в виде суммы простейших дробей: .

Далее:

В правой части приводим к общему знаменателю . Получаем , где -многочлен с неопределёнными коэф-ми. Из этого получаем .Приравнивая коэф-ты при одинаковых степенях, получаем систему лин. уравнений, из которой получаем искомые коэф-ты.

1) .

2)

3) ,

J₂:

4)

□ 1. Неопределенный интеграл. Свойства неопределенного интеграла

□ 2. Классы интегрируемых функций

□ 3. Замена переменной в неопределенном интеграле.

□ 4 . Интегрирование рациональных дробей

□ 5. Интегрирование простейших дробей 1, 2, 3 типов

1. Интеграл вида  , подстановкой  сводится к интегралу от рациональной функции относительно t.

2.  в этом случае заменой   , где s-наименьшее общее кратное чисел m..n.

3.     ;

    ;

    ;

4.  выделяем полный квадрат и подстановку 

5. ; ; : выделяем полный квадрат , и подстановку  .

1) Универсальная тригон-я подстановка.:

2) если ф.:

а) нечётна отн sinx (), то t=cosx;

б) нечётна отн cosx (), то t=sinx;

в) чётна отн cosx и sinx (), то t=tgx;

3)

а) t=sinx, n- целое “+” нечётное число б)t=cosx, m-целое “+” нечётное число в)t=tgx, m+n- чётное “-“ целое число г)формулы понижения порядка если m и n – целые неотрицат. чётные числа.

   

.

4) тригонометрич преобразования

.

 ,

  ,

  .

Выражается если:

1) p-целое число  , где k –наименьшее общее кратное дробей m и n.

2)  – целое число  , где s-знаменатель дроби p.

3) – целое число , где s-знаменатель дроби p.

Во всех остальных случаях такие интегралы «не берутся».

Всякое подынтегральное выражение можно представить в виде , где -ф. переем-й интегрирования.

Интегрированием по частям наз-ся сведение к .

Th. Пусть дифференцируемы на <a,b> и , тогда сущ-ет ;.

Пример:

Пусть функция определена на отрезке [a,b].

1) Точками a=x₀…x_n=b разобьём торезок на n отрезков.

2) В каждом отрезке выберем произвольную точку , и вычислим значение ф. в ней .

3) умн-м . на длину отрезка :

.

4) Cоcтавим сумму из всех произведений (интегральная сумма):

5) Обозначим через λ  длину наибольшего частичного отрезка  данного разбиения.

Определенным интегралом от функции   на отрезке  называется конечный предел I интегральной суммы , если такой предел существует:.

□ 6. Интегрирование иррациональных выражений

□ 7. Интегрирование тригонометрических функций

□ 8. Интегрирование дифференциального бинома

□ 9. Интегрирование по частям

□ 10. Интегральная сумма. Понятие определенного интеграла

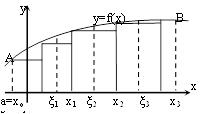
Найдем площадь:

1) разобьем отрезок  [a,b]  на n частей точками a = xo < x1 < x2 <…< xi-1 < xi <..< xn = b.

2) через точки деления проведем прямые параллельные оси Оу. В каждом частичном отрезке

[Xo , X1] , [ X1,X2 ] , … [ Xi-1, Xi ] … [ Xn-1, Xn ]   выберем произвольные точки

Найдем значения функции в этих точках  ƒ(ζ1), ƒ(ζ2), ƒ(ζi), ƒ(ζn),   и найдем сумму площадей прямоугольников с основанием  Δхi =  хi – хi-1,  i=1,n .

Сумма площадей прямоугольников равна:

, за площадь криволинейной трапеции принимается предел, к которому стремится эта сумма:

.

Т.е.

Геометрический смысл определенного интеграла: Определенный интеграл от не отрицательной ф-ии равен площади соответствующей криволинейной трапеции.

Обозначим через  и  точные нижнюю и верхнюю границы для функции  в -том частичном промежутке .

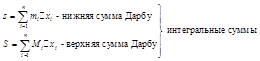Из определений нижней и верхней границ имеем , поэтому умножив все части неравенства на  и просуммировав их, получим .

При заданном разбиении промежутка суммы Дарбу  и  служат точными нижней и верхней границами для интегральных сумм.

Теорема.

Для того, чтобы определенный интеграл существовал, необходимо и достаточно, чтобы .

1)

2)

3)

4) Если [a,b] точкой c делится на 2 отрезок [a,c]  и [c,b], то

 =  + .

5) Если на отрезке [a,b] ƒ₁(х)≥ ƒ₂(х), то .

6) Если функция непрерывна на [a,b], то найдется точка ,такая что :

 =c (b – a);

7) ≤

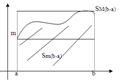
8) Если функция  y = ƒ(х) непрерывна на отрезке [a,b], то

m(b-a) ≤ ≤ M(b-a); m-наим-ее значение ф. M-наиб. на отрезке на [a,b].

Если функция  y = ƒ(х) непрерывна на отрезке [a,b] (m-наим-ее значение ф. M-наиб. на отрезке на [a,b]), то

m(b-a) ≤ ≤ M(b-a);.

.

.

Геом смысл:

Пусть  – непрерывная функция на отрезке  , функция  непрерывна и дифференцируема на ,и .Тогда верна формула .

Доказательство: По формуле Ньютона-Лейбница

где– первообразная для  на. Т.к. . То является первообразной для функции. Поэтому, согласно формуле Ньютона-Лейбница получаем:

.

□ 11. Определенный интеграл. Механический и геометрический смысл

□ 12. Суммы Дарбу

□ 13. Свойства определенного интеграла

□ 14. Оценка интеграла

□ 15. Замена переменной в определенном интеграле

Определенный интеграл можно выразить многообразными геометрическими и физическими величинами. При этом применяется следующая единообразная схема:

1) искомая величина  ставится в соответствие с промежутком  некоторого изменения аргумента;

2) промежуток  разбивается на части  (в дальнейшем будем считать , а длины промежутков ). Пусть искомая величина  распадается на части , причем ;

3) в качестве типичного представителя частей  берется одна из них . Она выражается (исходя их условия задачи) приближенной формулой следующего вида: ;

4) с увеличением числа  погрешность  должна стремиться к нулю, поэтому искомая величина  есть предел этой суммы, т.е. .

Пусть на отрезке [a;b] ф-я y = f(x) неотрицательна.

Тогда S_{крив. трап.}, огран. этой кривой, осью

ОХ и прямыми х=а, х=b ,  S = ∫ f(x)dx

Если f(x)≤0, то  -S = ∫ f(x)dx , S = - ∫ f(x)dx

Если ф-я - конечное число раз меняет знак на отр. [a;b], то  инт-л по всему отр. разбиваем на сумму инт-лов по частичн. отрезкам. S=∫│f(x)│dx.

Если же требуется найти S фигуры, ограничен. кривыми y=f₁(x) и y=f₂(x), причем f₁(x) £ f₂(x) на отрезке [a;b], то S=∫[ f₂(x) - f₁(x) ]dx

ПАРАМЕТРИЧЕСКИ:

,

.

ДАЛЕЕà

Пусть  неопределенная функция, имеющая неопределенную производную. Ее графиком является линия. Длиной дуги кривой линии назовем предел, к которому стремится длина вписанной в нее ломаной при неограниченном увеличении числа ее сторон и при стремлении наибольшей из этих сторон к нулю.

Итак, пусть линия  задана уравнением .

Разобьем промежуток  на  частей точками . Проведя через каждые две последовательные точки деления дуги хорды